Table of Contents
GS2-660-C4-51~57
不得不说660的题目太综合了,这几道不定积分的计算题综合性都比较强,里面很多点值得取深究。 并且涉及到很多基本公式得掌握,要多体会体会!
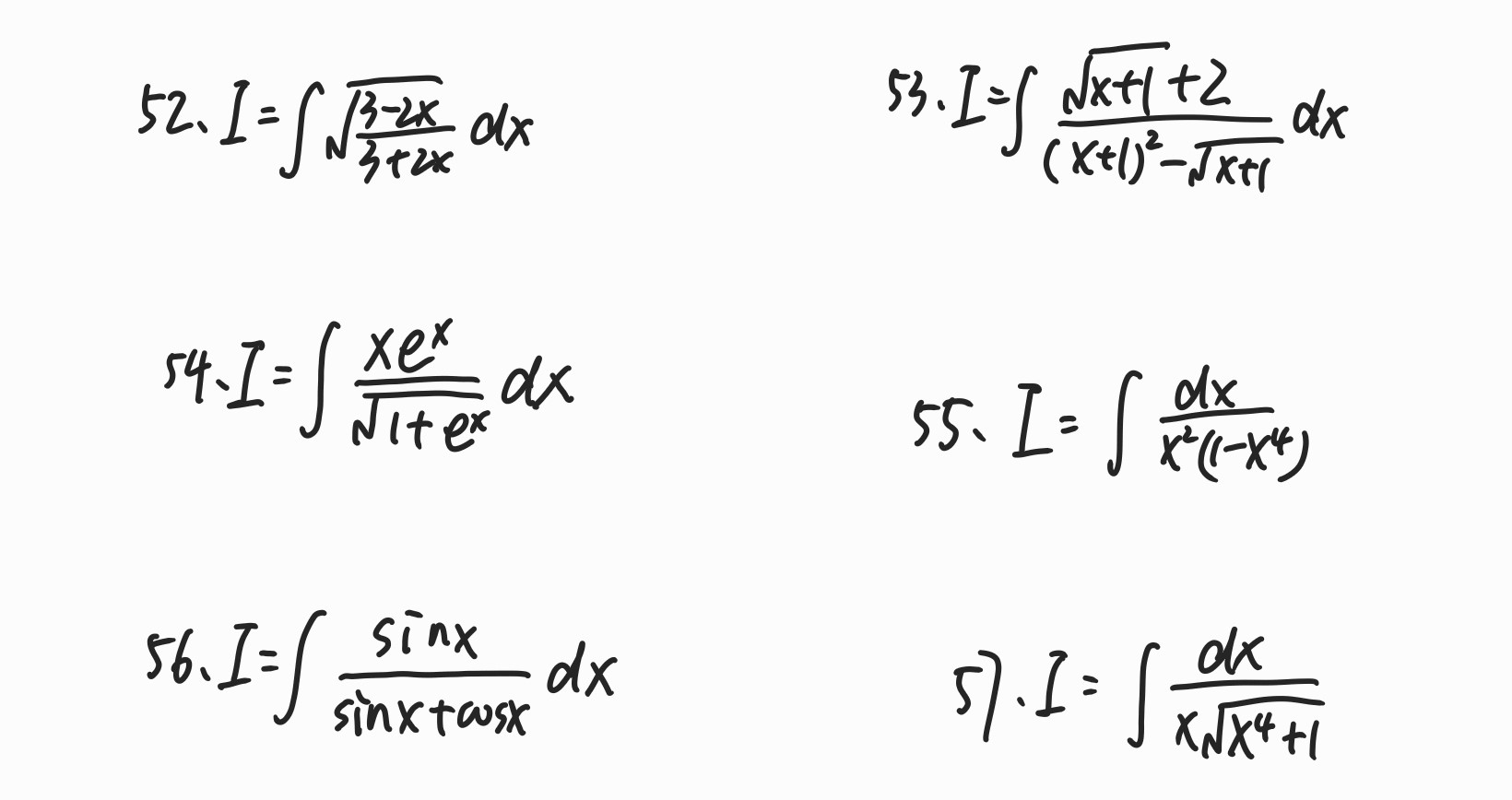
数据结构-图(一)
逻辑结构和定义
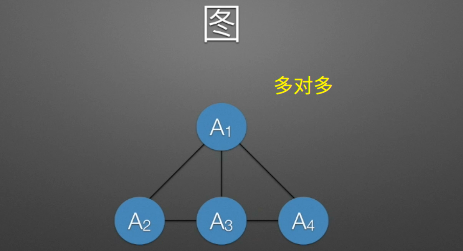
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中G表示一个图,V是图G中顶点的集合,E是图G中边的集合
- 线性表中数据元素叫元素,树中将数据元素叫结点,图中数据元素称之为顶点(Vertex)
- 线性表中可以没有数据元素,称为空表。树中可以没有结点,叫做空树。在图结构中,不允许没有顶点。在定义中,若V是顶点的集合,则强调了顶点集合V有穷非空
- 线性表中,相邻的数据元素之间具有线性关系,树结构中,相邻两层的结点具有层次关系,图中任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的
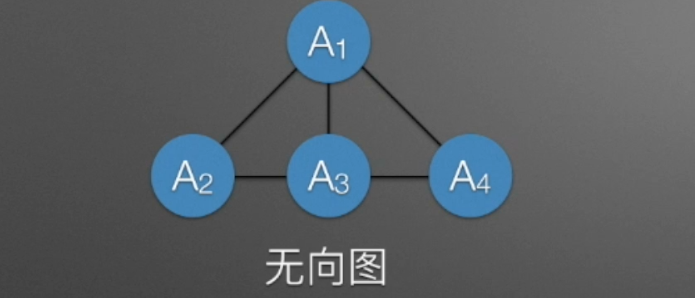
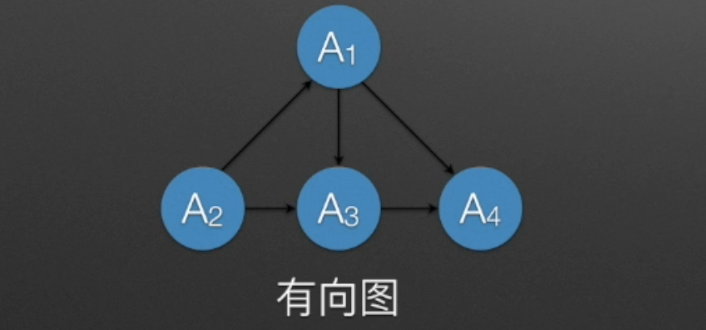
| 无向图 | 有向图 |
|---|---|
| 每条边都没有方向 | 每条边(弧)都有方向 |
| 边(A1,A3) | 弧(A1,A3) |
| 顶点A1的度为3 | 顶点A1的入度为1,出度为2,度为3 |
一些概念
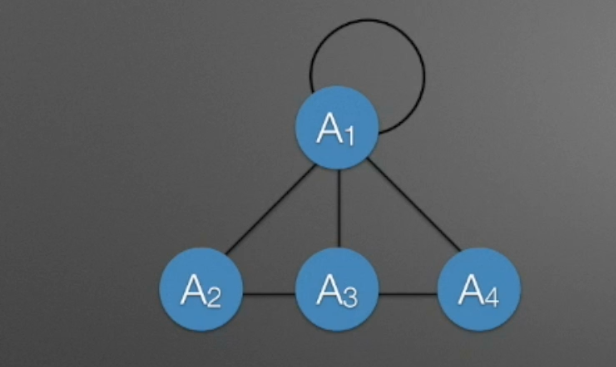
简单图
在图中,若不存在某顶点到其自身的边,且不存在重复的边,则称之为简单图。下面都不是简单图。
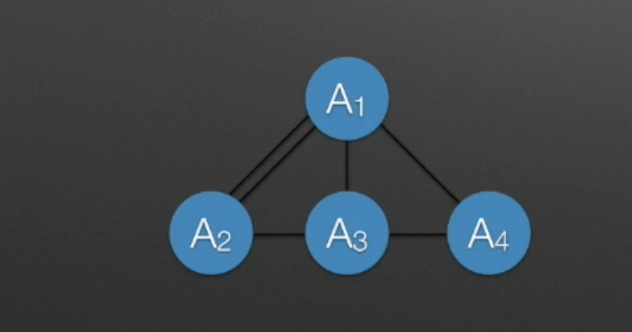
完全图
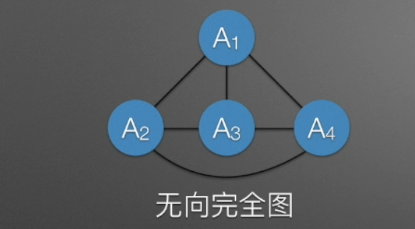
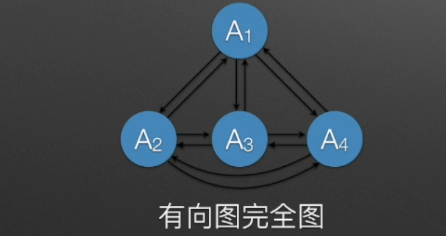
- 在无向图中,若任意两顶点之间存在边,则称之为无向完全图,这种图边的个数位n(n-1)/2,n为顶点数。
- 在有向图中,若任意两顶点之间存在方向相反的两条边,则称之为有向完全图,这种图边的个数位n(n-1),n为顶点数。
带权图
在图中,若边含有权值,则一般称之为网(本课程中统称为图)。
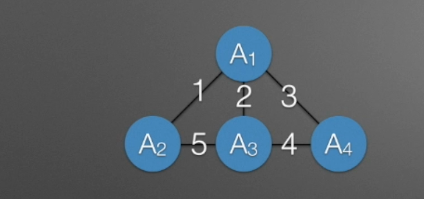
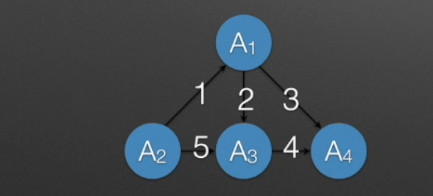
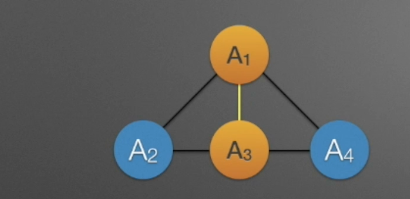
子图
下图图黄色部分为其所在图的子图(Subgraph)。
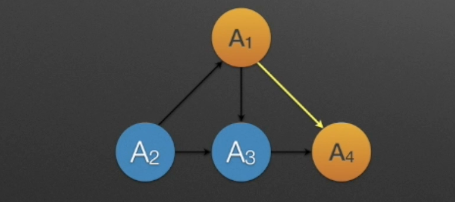
路径
路径是一个顶点到另一个顶点的顶点序列,路径长度是路径上边的个数。
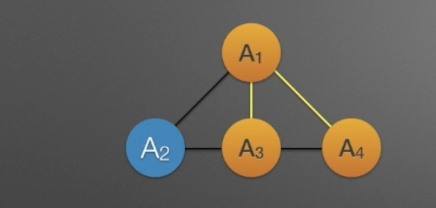
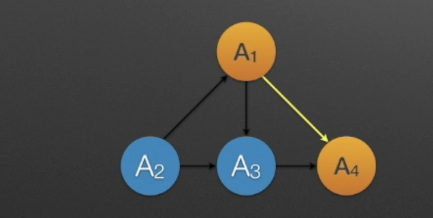
环
第一个顶点到最后一个顶点相同的路径称之为回路或者环。
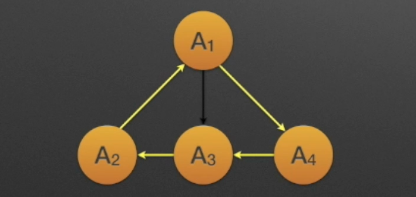
简单路径
序列中顶点不重复出现的路径称之为简单路径。
下面的就不是简单路径!,因为A3出现了2次。
路径序列:A1、A3、A6、A7、A4、A3、A5、A2
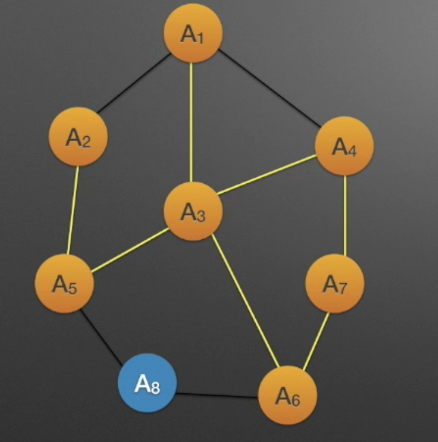
简单环
序列中除了第一个和最后一个顶点,其余顶点都不重复出现的环称之为简单环。下面的就不是简单环!
路径序列:A1、A3、A6、A7、A4、A3、A5、A2、A1
连通图
无向图中,如果$v_i$到$v_j$有路径,则称$v_i$和$v_j$连通;如果图中任意一对顶点连通,则此图为连通图。

连通分量
无向图中的极大连通子图称之为连通分量。

强连通图
有向图中,每一对$v_i$到$v_j$,从$v_i$到$v_j$,和从$v_j$到$v_i$都存在路径则称强连通图。

强连通分量
有向图中的极大连通子图称之为强连通分量。

例题

- 对于I,可举例说明,如下图,1个顶点,两个顶点,三个顶点的时候所有顶点的度之和都为偶数


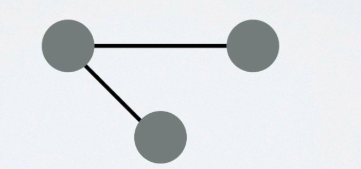
- 对于II,举反例即可,如上图中第三个,边数是等于顶点个数减1的,并非大于。
- 对于III,下图中则不满足。所以只有I是对的。
图的顺序存储结构-邻接矩阵存储法
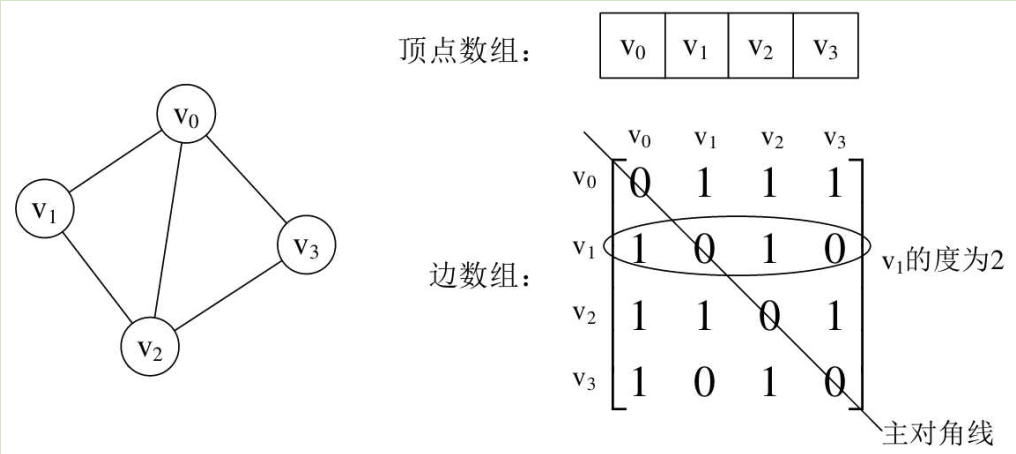
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息
有向无权图
设图G有n个顶点,则邻接矩阵是一个n×n的方阵,定义为:
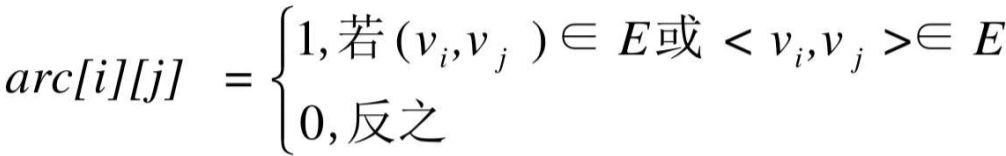

有了这个矩阵,很容易知道图中的信息:
- 判定任意两顶点是否有边无边
- 要知道某个顶点的度,就是这个顶点$v_i$在邻接矩阵中第i行(或第i列)的元素之和。
- 求顶点$v_i$的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[i][j]为1就是邻接点
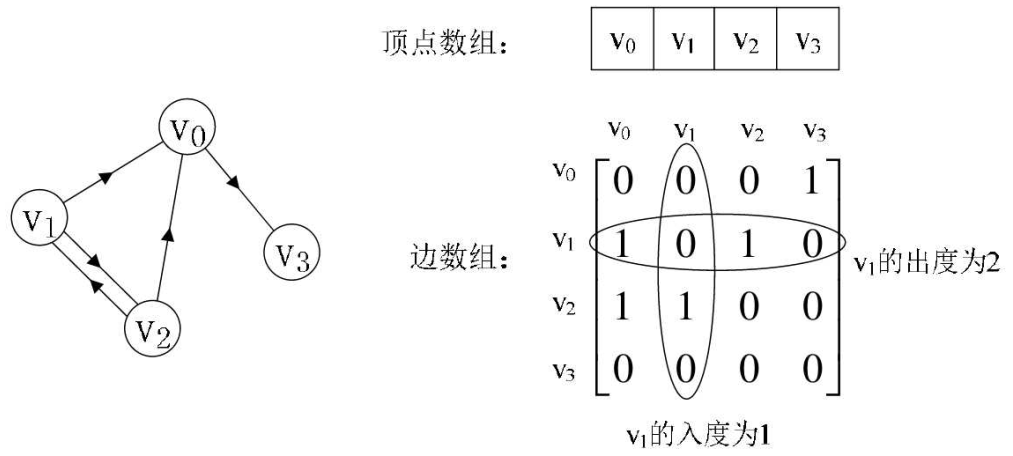
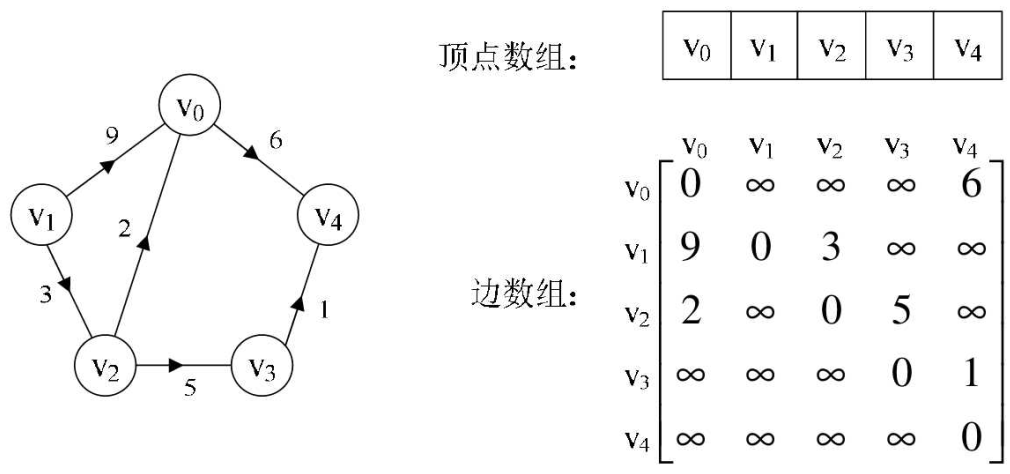
顶点数组为$verte[4]={v_0,v_1,v_2,v_3}$,弧数组arc[4][4]为右图的一个矩阵。主对角线上数值依然为0。但因为是有向图,所以此矩阵并不对称
有向图讲究入度与出度,顶点$v_1$的入度为1,正好是第$v_1$列各数之和。顶点$v_1$的出度为2,即第$v_1$行的各数之和
判断顶点$v_i$到$v_j$是否存在弧,只需要查找矩阵中arc[i][j]是否为1。求的所有邻接点就是将矩阵第i行元素扫描一遍,查找arc[i][j]为1的顶点
有向有权图
设图G是网图,有n个顶点,则邻接矩阵是一个n×n的方阵,定义为:
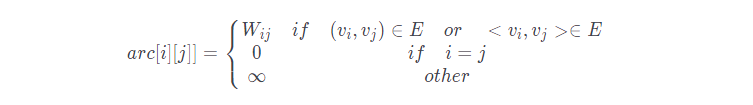
$w_{ij}$表示$(v_i,v_j)$或$<v_i,v_j>$上的权值∞表示一个计算机允许的、大于所有边上权值的值,也就是一个不可能的极限值
实现带权图c语言描述:
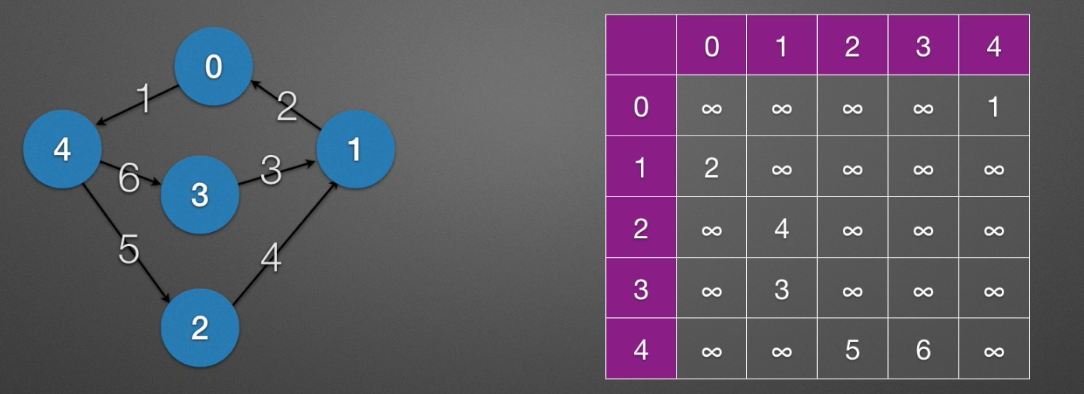
float MGraph[5][5];
for (int i = 0; i <5 ; ++i)
for(int j = 0; j<5;++j)
MGraph[i][j] = MAX;
但是如果顶点不是连续的或者顶点根本不是数字呢?可以专门搞一个顶点数组,则二维数组的行标或者列标恰好和一维数组的下标对应
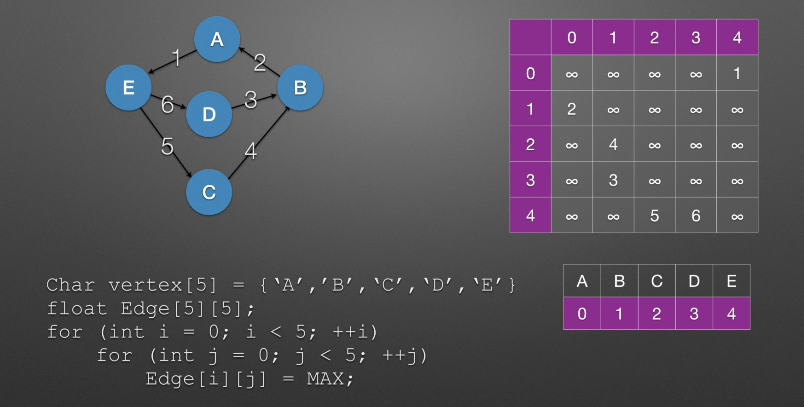
char vertex[5] = ['A','B,'C',D','E'];
float Edge[5][5];
for (int i=o; i<5 ;++i)
for(int j=0; j<5; ++j)
Edge[i][j] = MAX;
邻接矩阵例题
- 408,13年07题

【分析】:观察矩阵元素,可知为有向图,因为矩阵不对称。矩阵中对于每一个顶点都有它的一行和一列,对于它所属的那一行,其中1的个数代表它所发出的边的条数;而对于它所在的列,其中1的个数代表指向它的边的条数,而对于一个顶点,它的度数就是入度和出度的总和,即它发出的边和指向它的边的总和,因此对于每一个顶点在邻接矩阵中,数一下它所在行列的1的个数就是它的度。如下图,可知答案为C。

- 综合题
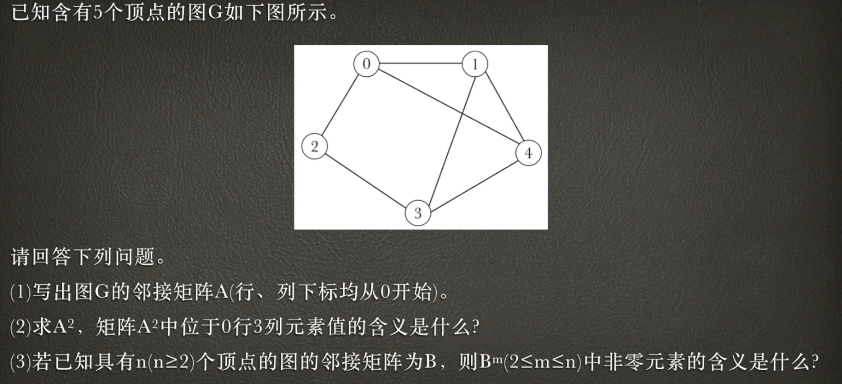
- 【分析】,这是一个无向无权图。且行列下标都是从0开始,那么很容易写出这么一个矩阵。
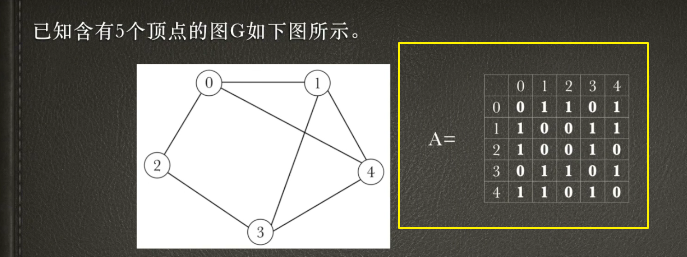
- 【分析】。先求出
A^2。如下图,那么0行3列是怎么得来的?可知是A的第零行与A的第三列相乘的得到,即把所有的$A_{0,k}$和$A_{k,3}$相乘的结果相加。$A_{0,k}$代表顶点0到顶点k有没有边,为0就是没有边,为1就是有边;$A_{k,3}$就是从顶点k到顶点3有没有边,那这个乘积什么时候为1,很明显两边都为1才为1,此时代表从0到3可以经过中间结点k到达,那把所有这些$A_{0,k}$和$A_{k,3}$相乘的结果相加则代表,图中从顶点0到顶点3只有一个中间顶点的条数为有3条

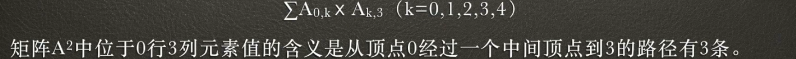
- 【分析】很明显为第二问的一般情况。则为
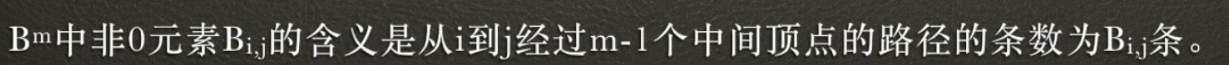
图的链式存储结构-邻接表
数组与链表相结合的存储方法称为邻接表(Adjacency List)。
邻接表的处理办法:
- 图中顶点用一个一维数组存储,对于顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息
- 图中每个顶点$v_i$的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表存储,无向图称为顶点$v_i$的边表,有向图则称为顶点$v_i$作为弧尾的出边表。
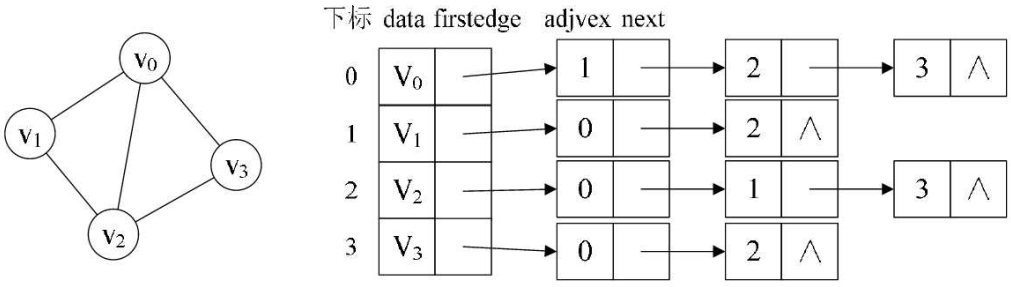
顶点表的各个结点由data 和 firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点,即此结点的第一个邻接点
边表结点由adjvex和next 两个域组成,adjvex 是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针
要想知道某个顶点的度,就去查找这个顶点的边表中结点的个数。若要判断顶点$v_i$到$v_j$是否存在边,只需要测试顶点$v_i$的边表中adjvex是否存在结点$v_j$的下标j就行了。若求顶点的所有邻接点,其实就是对此顶点的边表进行遍历,得到的adjvex域对应的顶点就是邻接点
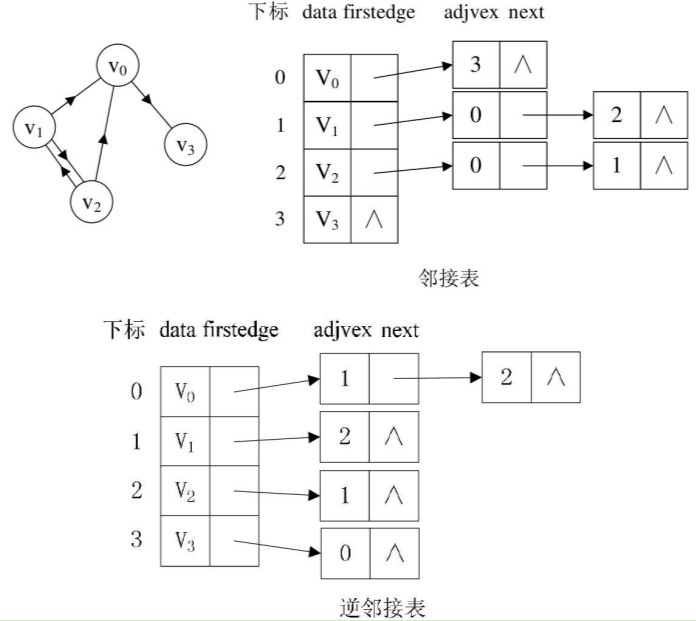
若是有向图,第一幅图的邻接表就是第二幅图。有向图由于有方向,是以顶点为弧尾来存储边表的,很容易得到每个顶点的出度。有时为了便于确定顶点的入度或以顶点为弧头的弧,可以建立一个有向图的逆邻接表,即对每个顶点$v_i$都建立一个链接为$v_i$为弧头的表
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域存储权值信息
结点定义的代码:
typedef char VertexType; //顶点类型,由用户定义
typedef int EdgeType;
typedef struct EdgeNode //边表结点
{
int adjvex; //邻接点域,存储该顶点对应的下标
EdgeType weight; //用于存储权值,对于非网图可以不需要
struct EdgeNode *next;//链域,指向下一个邻接点
}EdgeNode;
typedef struct VertexNode //顶点表结点
{
VertexType data; //顶点域,存储顶点信息
EdgeNode *firstedge; //边表头指针
}VertexNode,AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numVertexes,numEdges; //图中当前顶点数和边数
}GraphAdjList;
无向图的邻接表创建代码:
/* 建立图的邻接表结构 */
void CreateALGraph(GraphAdjList *G)
{
int i,j,k;
EdgeNode *e;
printf("输入顶点数和边数:\n");
scanf("%d,%d",&G->numVertexes,&G->numEdges);//输入顶点数和边数
for(i=0;i<G->numVertexes,i++)
{
scanf(&G->adjList[i].data);//输入顶点信息
G->adjList[i].firstedge=NULL;//将边表置位空表
}
for(k=0;k<G->numEdges;k++)
{
printf("输入边(vi,vj)上的顶点序号:\n");
scanf("%d,%d",&i,&j);//输入边(vi,vj)上的顶点序号
e=(EdgeNode *)malloc(sizeof(EdgeNode));/*向内存申请空间,生成边表结点*/
e->adjvex = j;//邻接序号为j
e->next = G->adjList[i].firstedge;//将e指针指向当前顶点指向的结点
G->adjList[i].firstedge = e;//将当前顶点的指针指向e
e=(EdgeNode *) malloc(sizeof(EdgeNode));/*向内存申请空间,生成边表结点*/
e->adjvex = i;//邻接序号为i
e->next=G-adjList[j].firstedge;//将e指针指向当前顶点指向的结点
G->adjList[j].firstedge = e;//将当前顶点的指针指向e
}
}对于无向图,一条边对应都是两个顶点,所以在循环中,一次就针对i和j分别进行了插入。本算法的时间复杂度,对于n个顶点e条边来说是$O(n+e)$。
邻接表的缺陷:
- 关心了出度问题,想了解入度就必须要遍历整个图才能知道
- 逆邻接表解决了入度却不了解出度的情况
图的链式存储结构-十字链表
十字链表(Orthogonal List):把邻接表和逆邻接表结合起来的存储方式。
重新定义顶点表结点结构如下:
| data | firstin | firstout |
|---|
firstin表示入边表头指针,指向该顶点的入边表中第一个结点,firstout表示出边表头指针,指向该顶点的出边表中的第一个结点
重新定义的边表结点结构如下:
| tailvex | headvex | headlink | taillink |
|---|
顶点依然是存入一个一维数组$v_0,v_1,v_2,v_3$,实线箭头指针的图示邻接表相同。以顶点$v_0$来说,firstout指向的是出边表中的第一个结点$v_3$。所以边表结点的headvex=3,而tailvex其实就是当前顶点$v_0$的下标0,由于$v_0$只有一个出边顶点,所以headlink和taillink都是空.
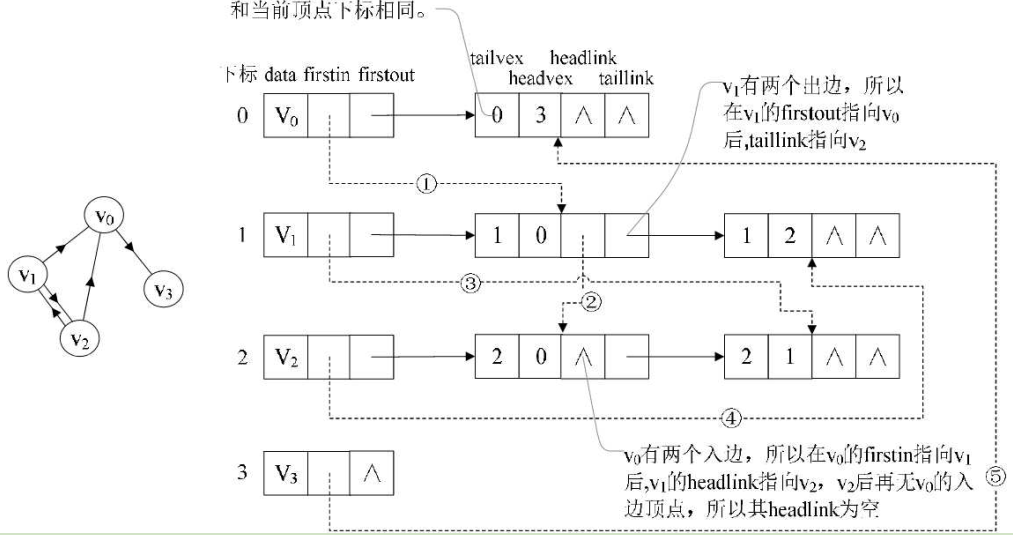
虚线箭头的含义此图的逆邻接表的表示。$v_0$有两个顶点$v_1$和$v_2$的入边。因此$v_0$的firstin指向顶点$v_1$的边表结点中headvex为0的结点,如图中的①。接着由入边结点的headlink指向下一个入边顶点$v_2$,如图中的②。对于顶点,它有一个入边顶点,所以它的firstin指向顶点$v_2$的边表结点中headvex为1的结点,如图中的③。顶点$v_2$和$v_3$也是同样有一个入边顶点,如图中④和⑤
十字链表的好处:
- 把邻接表和逆邻接表整合在了一起,容易找到以$v_i$为尾的弧和以$v_i$为头的弧,容易求得顶点的出度和入度
- 除了结构复杂一点外,创建图算法的时间复杂度和邻接表相同的
图的链式存储结构-邻接多重表
重新定义的边表结点结构如下:
| ivex | ilink | jvex | jlink |
|---|
ivex和jvex是与某条边依附的两个顶点在顶点表中的下标。ilink指向依附顶点ivex的下一条边,jlink指向依附顶点jvex的下一条边。这就是邻接多重表结构
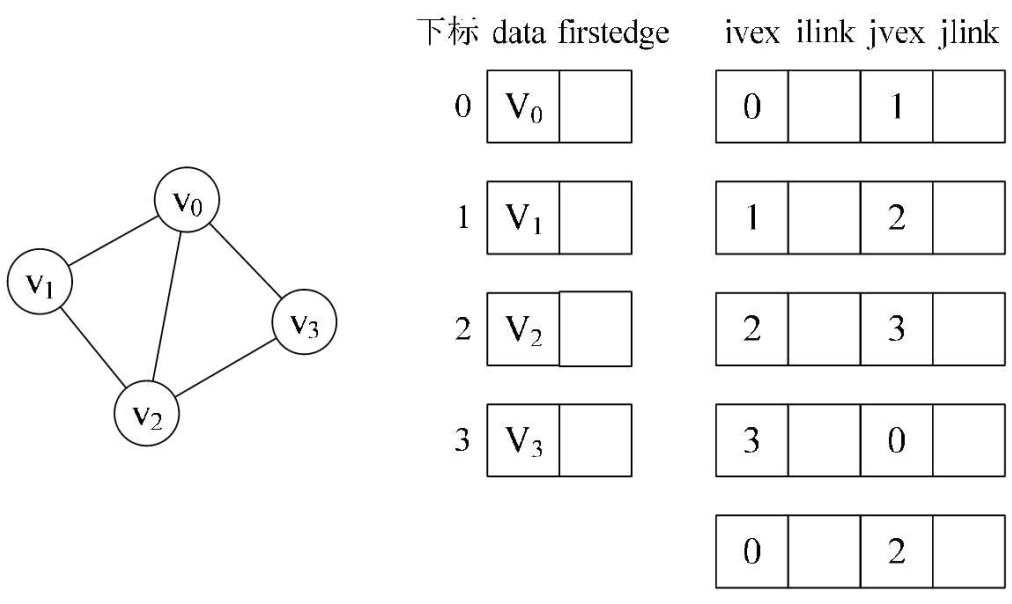
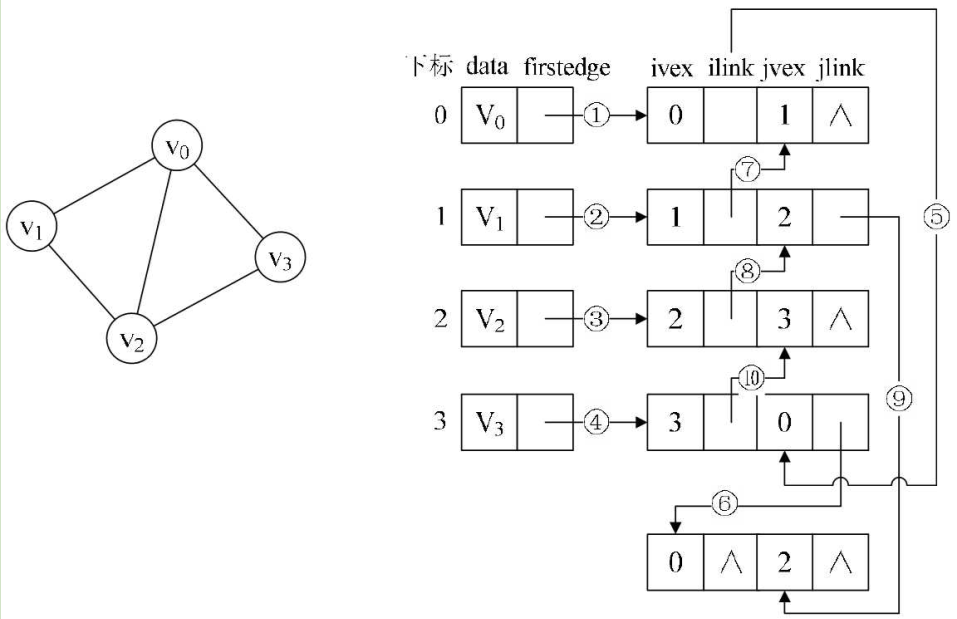
首先连线的①②③④就是将顶点的firstedge指向一条边,顶点下标要与ivex的值相同,接着,由于顶点$v_0$的$(v_0, v_1)$边的邻边有$(v_0, v_3)$和$(v_0, v_2)$。因此⑤⑥的连线就是满足指向下一条依附于顶点v 的边的目标,ilink指向的结点的jvex一定要和它本身的ivex的值相同。连线⑦就是指$(v_1, v_0)$这条边,相当于顶点v指向$(v_1, v_2)$边后的下一条。$v_2$有三条边依附,所以在③之后就有了⑧⑨。连线@⑩的就是顶点$v_3$在连线④之后的下一条边。左图一共有5条边,所以右图有10条连线。
邻接多重表和邻接表的区别:同一条边在邻接表中用两个结点表示,在邻接多重表中只有一个结点。若要删除左图$(v_0,v_2)$的这条边,只需要将右图的⑥⑨的链接指向改为∧即可。
恋词U13
- forge v.锻炼;伪造;努力加强;稳步前进
- orphan n.孤儿
- deed n.行为;行动;契约;证书
- deem v.认为;视为;相信
- distract v.分散(注意力);使分心;迷惑;扰乱
- contractor n.承包商;承包者
- subconscious adj.下意识地;潜意识的
- heal v.使治愈;愈合;和解
- upheaval n.激变;剧变;动乱;动荡
- novelty n.新奇事物
- heroin n.海洛因
- pharmaceutical adj.制药的;药物的
- slot n.狭缝;扁口;位置 v.使有位置;把..放入狭长孔
- slum n.贫民窟;贫民区;破旧房
- slump n.骤减;锐减;萧条期;衰退 v.骤减;锐减
- aerial adj.航空的;空中的 n.天线
- aviation n.航空;飞行
- tempt v.引诱;鼓动;吸引
- aesthetic adj.美学的;艺术的;审美的
- submit v.屈服;顺从;投降;呈送;提交
- emit v.发出;发射;散发
- perplexing adj.复杂的;令人困惑的
- intricate adj.错综复杂的;难理解的