Table of Contents
闲聊
怀念哥哥
吃早餐的时候才发现今天是愚人节,听了首哥哥的歌。
恋词U6
- triumph n.v胜利;得胜
- consent v.n 同意;赞成
- inferior adj.低等的;下级的;质量差的 n。下级
- jurisdiction n.司法权;审判权;管辖区域
- legislation n.法律,法规,立法
- legislative adj.立法的;制定法律的
- legitimacy n.合法性;合理性;正当性
- legitimate adj.合法的;正当的;合理的
- lawsuit n.诉讼,起诉
- mature adj.成熟的;熟的;酿成的;成年的
- disorder n.混乱;骚乱;(身心机能)失调;紊乱
- revenue n.收入;税收
- levy v.征收;收取 n.税额,税款
- cyberspace n.计算机空间,网络空间
- bypass n.旁道;旁路;心脏搭桥手术 v.绕过;避开
- compass n.指南针;罗盘;圆规
- discourse n.论文;演讲;谈话 v.演讲,讲述
- scale n.刻度;天平;比例尺;规模;音阶;鱼鳞;等级 v.缩减;减小
- amid prep.在...中间;在..之中
- on short notice 迅速;立即
- notion n.看法;观念;理念;概念
- notorious adj.臭名昭著的,声名狼藉的,众所周知的;
- denote v.意思是;预示;代表
- embody v.体现,使具体化;代表;包括;包含
- deputy n.代理人;代表 adj.副的;代理的
多元函数微分学(三)- 多元函数的极值于最值
无约束极值


条件极值及拉格朗日乘数法

最大最小值

常考题型与例题
不在这里展示。
田静语法-C1-S1-简单句的核心构成
来看田静的语法视频了,配上《句句真研》。
今晚看了第一章的第一节简单句的核心构成,是个很温柔的老师,和刘晓艳不同的风格,田静的课干货比较多。
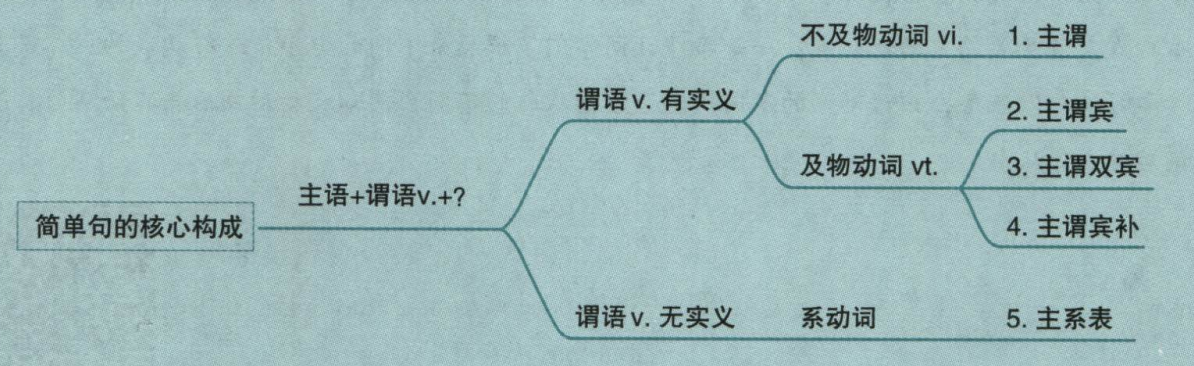
今晚的知识点都在这里啦。有点需要注意的
- 主谓结构的简单句并不是说后面完全不能接东西,而是说后面不需要接上动作的承受对象,当然可以额外补充时间、地点等。
课后习题
做题最能巩固知识点了。


数据结构-归并-线性表(八)
归并,顾名思义。就是将两个或者多个表按照某种规矩给他合并成一个。
(线性表这一章只研究二路归并,即将2个线性表归并成一个。)
顺序表归并
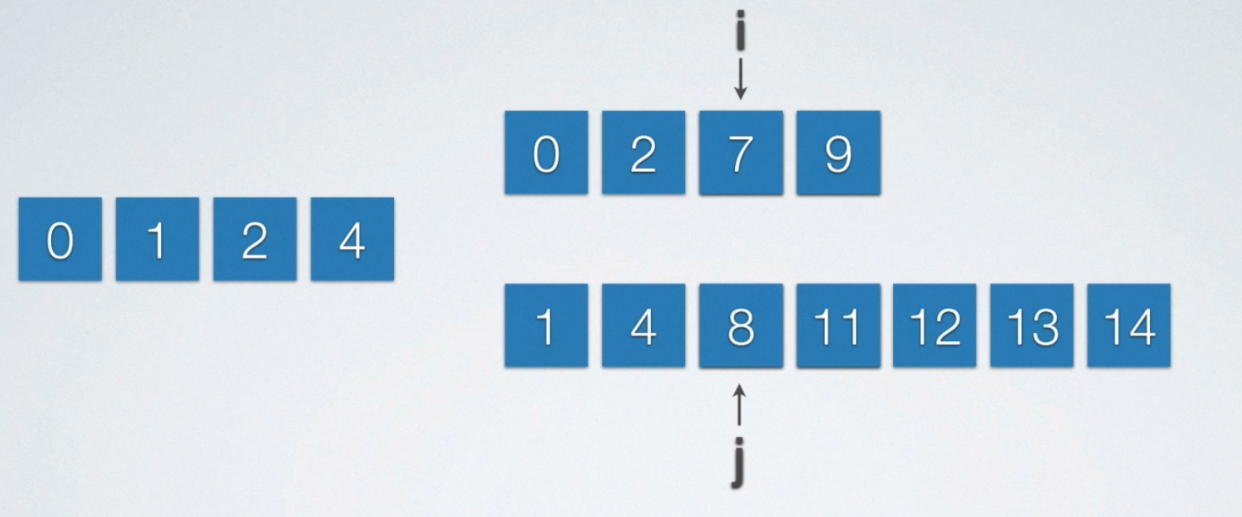
每次从线性表中挑出最小的元素,任何把它插入到当前所归并好的线性表的末端即可。由于待归并的两个顺序表是有序的,假设他们是升序。所以其最小的元素就在顺序表的最前端,所以呢,我们每次只需要让当前顺序表最前端的两个元素比较一下即可!
(详细还是看纸质笔记吧)。

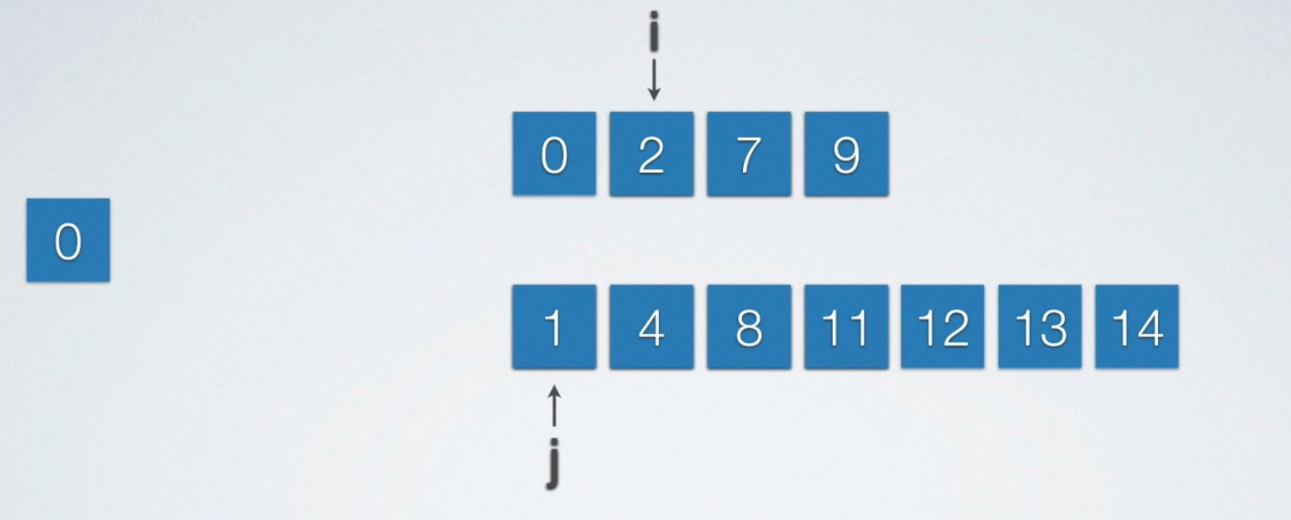
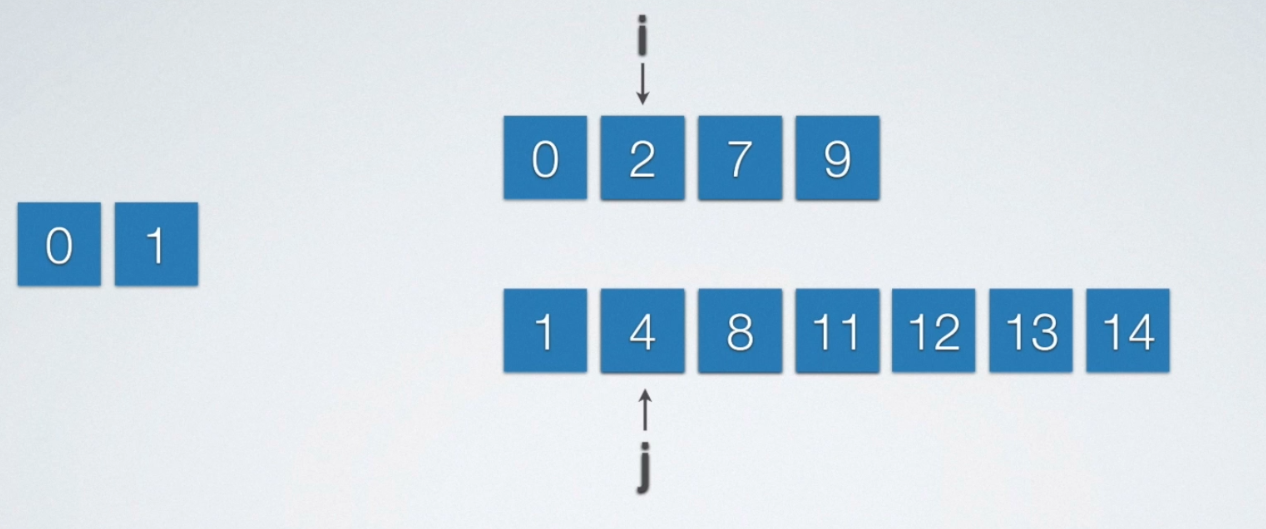
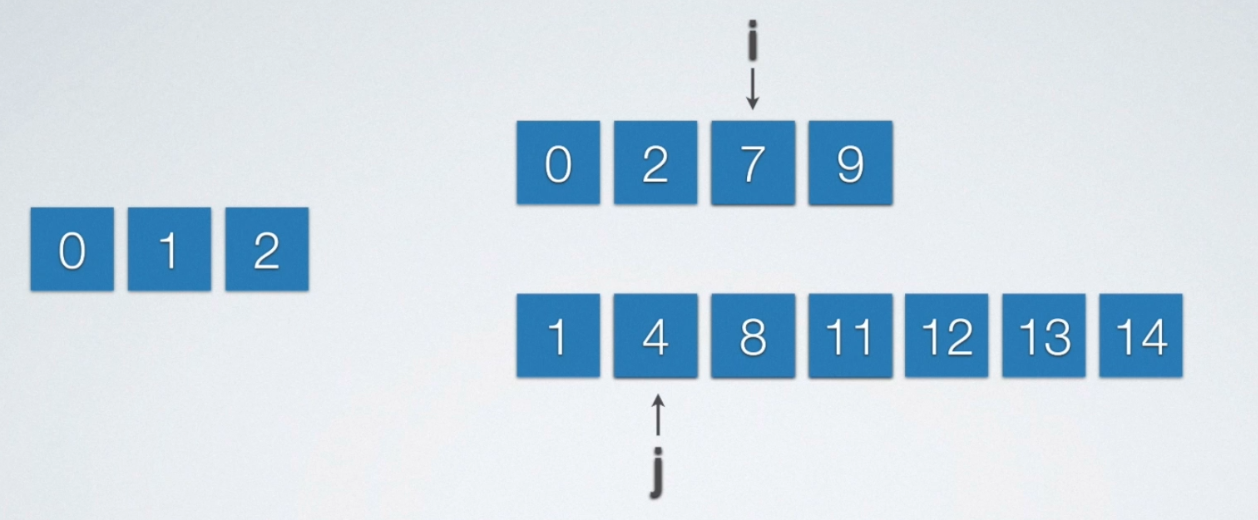







void mergearray(int a[], int m, int b[], int n, int c[])
{
int i = 0,j = 0;
int k = 0;
while(i < m && j < n)
{
if(a[i] < b[i])
c[k++] = a[i++]; // c[k] = a[i];k++;i++;
else
c[k++] = b[j++];
}
while(i < m)
c[k++] = a[i++];
while(j < n)
c[k++] = b[j++];
}
链表归并1
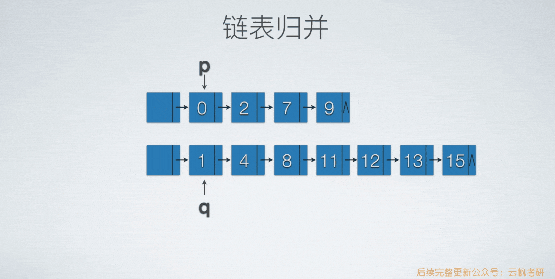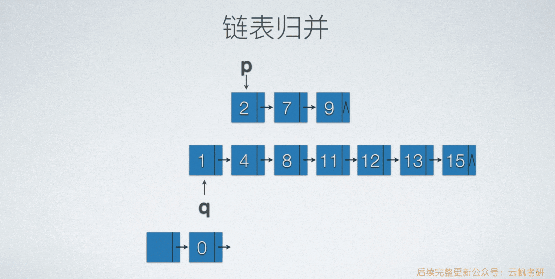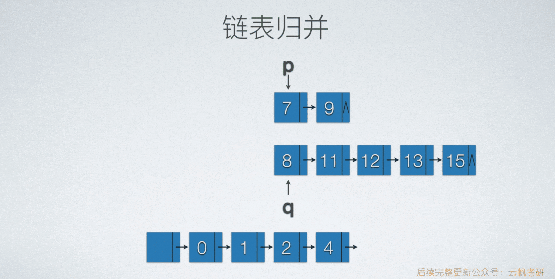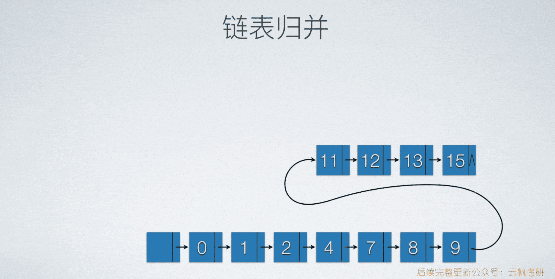
原理与顺序表类似。不需要开辟新的存储空间,而顺序表要。假设归并的是2个含有头结点的单链表,新链表的头结点不用重新生成,直接用两个两个链表中的任意一个头结点就好了。
void merge(LNode *A, LNode *B, LNode *&C)
{
LNode *p = A->next;
LNode *q = B->next;
LNode *r;
C = A;
C->next = NULL;
free(B);
r = C;
while( p != NULL && q != NULL)
{
if(p->data <= q->data)
{
r->next = p; p- = p->next;
r = r->next;
}
else
{
r->next = q; q->q->next;
r = r->next;
}
}
if(p != NULL) r->next = p;
if(q != NULL) r->next = q;
}
链表归并2
考虑另外一种情况,假如我想归并出一条和原来链表顺序相反的链表,应该怎么做呢?即原来链表做的假如是升序的,想归并得到一条按数据域降序的链表,应该怎么做呢?
void merge(LNode *A, LNode *B, *LNode *&C)
{
LNode *p = A->next;
LNode *q = B->next;
LNode *s;
C = A;
C->next = NULL;
free(B);
while( p != NULL && q != NULL)
{
if(p->data <= q->data)
{
s = p;p = p->next;
s->next = C->next; C->next = s;
}
else
{
s = q; q = q->next;
s->next = C->next;C->next = s;
}
}
while( p != NULL)
{
s = p;
p = p->next;
s->next = C->next;
C->next = s;
}
while( q != NULL)
{
s = q;
q = q->next;
s->next = C->next;
C->next = s;
}
}