Table of Contents
多元函数微分学(二)
复合函数微分法

不要死记公式,上面所用方法是链导法。可以画树状图去理解,如下图:
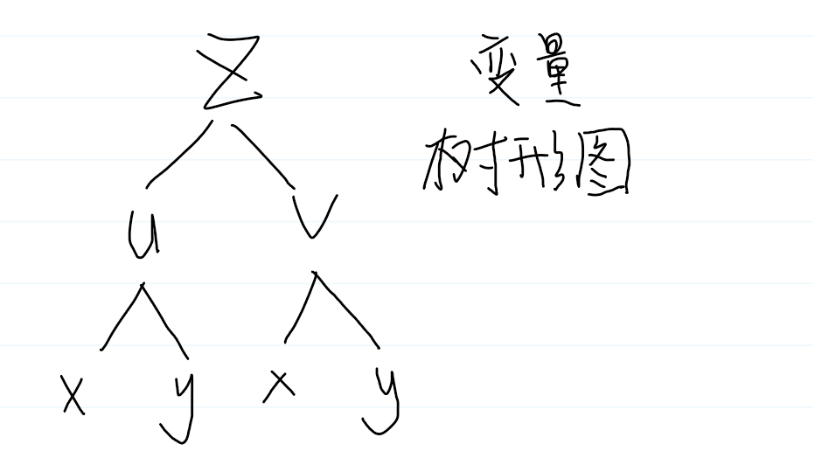
隐函数微分法


常考例题与题型
不在这里展示。
数据结构-划分-线性表(八)
考研中,划分规则特指以某个元素为标准,把线性表中的元素分为左右两个部分。
三种类型题目。
第一个元素为枢轴
给出一个顺序表:arr[7],第一个元素为枢轴将顺序表划分为左右两个部分,使得左边所有元素小于枢轴,右边的都大于枢轴。并且枢轴要夹在左右两部分之间。
void partition()int arr[], int n)
{
int temp;
int i = 0, j = n - 1;
temp = arr[i];
while(i < j)
{
while(i < j && arr[j] >= temp) --j;
if(i < j)
{
arr[i] = arr[j];
++i;
}
while(i < j && arr[i] < temp) ++i;
if(i < j)
{
arr[j] = arr[i];
--j;
}
}
arr[i] = temp;
}
有些要注意的点:
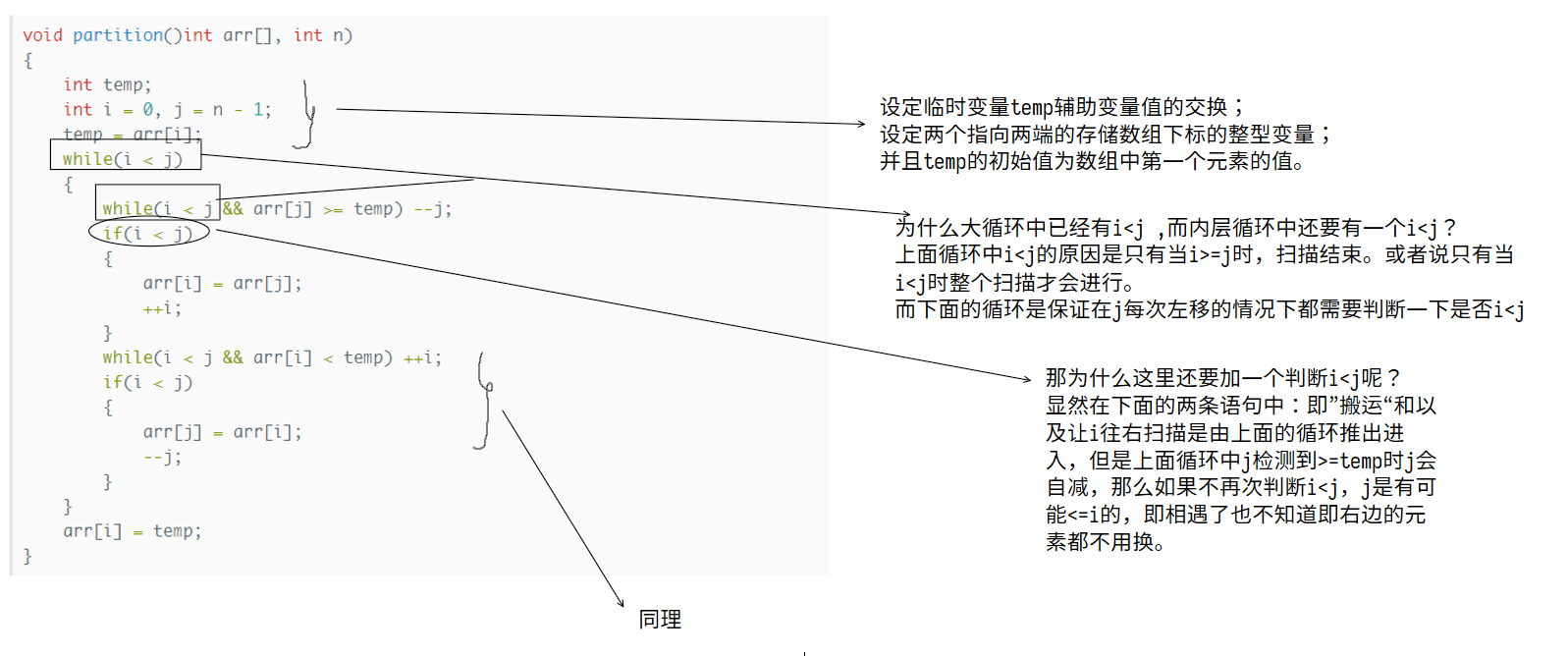
任意指定数为枢轴
当参与比较的值不等于
temp,即不等于数组的值,也就是说随便选一个其他的值来参与这里的比较时。
经过画图发现(图笔记有,不在这里画了)。假设comp = 0。
- 效果就是以0为界限分成了前后部分,前半部分小于0,后半部分大于等于0;
- i和j最终指向的值是2,而不是0,即指向的是枢轴。
总结一般情况:
假设temp = x, comp = y。
- 效果是把数组元素以
Y为界限分成了前后部分,前半部分小于Y,后半部分大于等于Y。 i和j最终指向的值是X,而不是Y。
数组中任意元素为枢轴
考虑这么一种情况,假如现在以数组中的任何一个位置上的元素来作为枢轴进行划分。假如写一个函数传入数组下标
k,就以k为位置上的元素为枢轴进行划分,该怎么去写这个函数呢。之前讲过第一个算法可以保证以数组中的第一个位置进行划分,怎么样在这个基础上改出想要的代码呢?
只需将你想要作为枢轴的元素给交换到第一个位置上来即可。
void partition()int arr[], int n,int k) //新增k位置元素整型变量
{
int temp;
int i = 0, j = n - 1;
///
temp = arr[0];
arr[0] = arr[k];
arr[k] = temp;
///元素交换操作
temp = arr[i];
while(i < j)
{
while(i < j && arr[j] >= temp) --j;
if(i < j)
{
arr[i] = arr[j];
++i;
}
while(i < j && arr[i] < temp) ++i;
if(i < j)
{
arr[j] = arr[i];
--j;
}
}
arr[i] = temp;
}