20210207

回顾 | 微分中值定理及导数应用（二） | 背单词

复习全书基础篇P45例5，解题关键在于找出极值点。而极值点就只有两种，一种是导数等于0的点，一种是不可导的点。从题目给出f'(x)的图像可看出导数等于0的点有三个，而根据极值判定中的充分条件的两侧变号即可判定极大极小值。而不可导的点则是0点，虽然0点不可导，但题目给出f(x)在0点连续，所以同样可以用刚才的判定条件判断0点的极值分类。
复习全书基础篇P45例6，可以采用排除法，用抽象函数具体化，不难看出分母等价于 ,极限为2，则可设f(x)为，所有问题都可以迎刃而解。
复习全书基础篇P45例7，求最大最小值的应用题，关键是找最简单的目标函数！因为要求导找极值点，所以如果觉得目标函数太过于复杂，不要盲目往下做，看看有没有更加简单的目标函数。然后按照求最大最小值的三步曲去做即可。
复习全书基础篇P45例8，具体函数怎么求拐点，一种就是二阶导数等于0的点，一种则是二阶导数不存在的点。又原函数定义域为x>0，所以求完二阶导之后没有不存在的点，所以令二阶导等于0求出拐点即可，然后再求拐点处的斜率即可。
复习全书基础篇P46例9，如果给出具体函数能画出图像直接画图像，如题，则是二次函数加了绝对值，很容易得到其图像，然后根据图像判定即可。

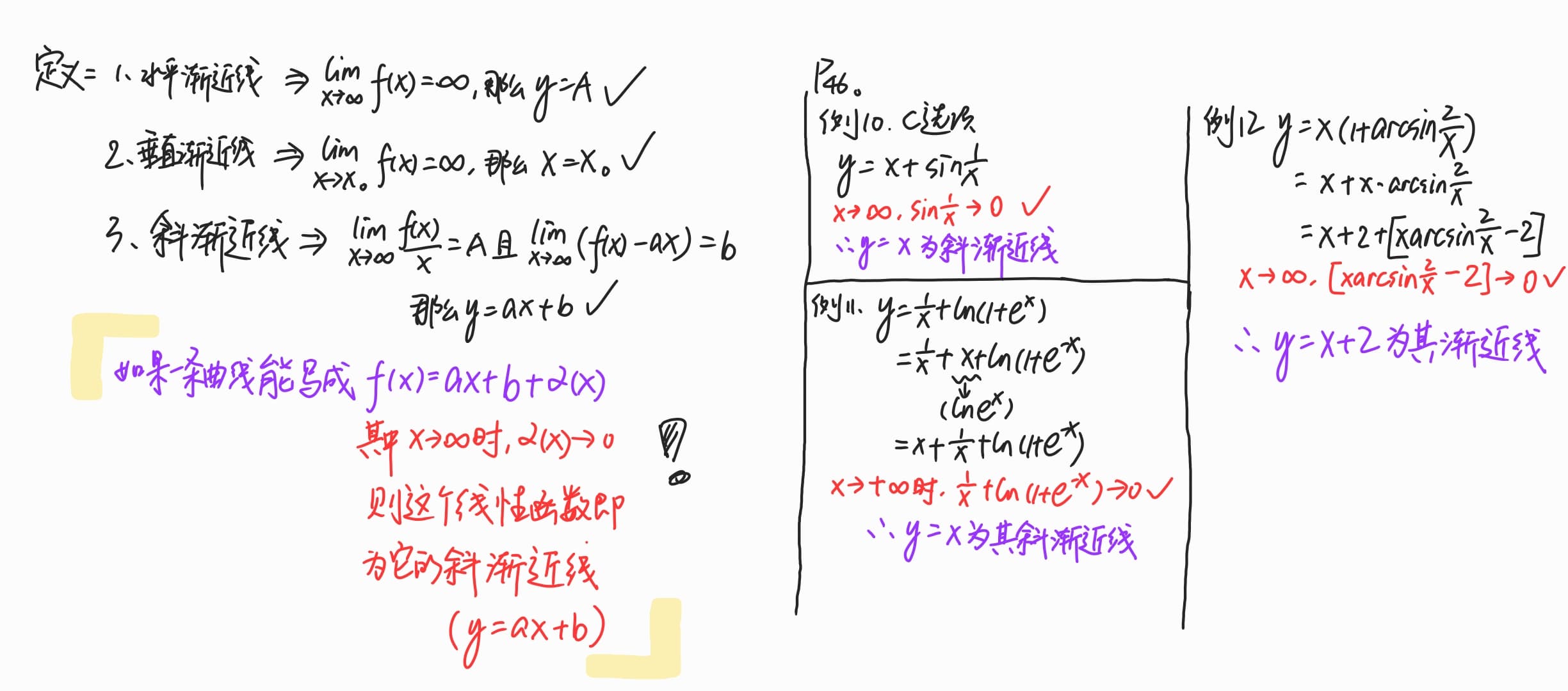
渐近线分为三种：水平渐近线、垂直渐近线和斜渐近线。如图，解题利用定义即可。
另外斜渐近线的判定有更加简便的方法，就一条曲线如果能写成y=ax+b+α(x)的形式，其中x->∞时，α(x)->0。即能写成一个线性函数加上一个x趋向于无穷时趋向于0的量，则这个线性函数就为这个曲线的斜渐近线。
- 复习全书基础篇P46例10，水平渐近线，垂直渐近线都能很快用定义求出，而斜渐近线可以利用上述方法迅速判定C选项是有斜渐近线的。
- 复习全书基础篇P46例11，这道题比较容易漏掉的是水平渐近线。任何时候看到x->∞,有e^∞都要留意要分类！这道题的斜渐近线的判定依旧可以使用上述方法。
- 复习全书基础篇P46例12，这道题则可直接利用第三种方法稍加变形就可写出斜渐近线。

首先理清一点，方程有根即f(x)=0，即f(x)有零点。

方程的根的存在性问题
- 运用零点定理：f(x)在[a,b]上连续，且f(a)·f(b)<0,则函数y= f(x)在区间(a,b)内有一个零点。就是两个条件：在[a,b]连续，两端点函数值异号即可证明存在（至少一个）。
- 运用罗尔定理，找到一个F(X)，使得F'(X)=f(x)，那么此时如果在[a,b]上连续，在(a,b)可导，且F(a)=F(b),那么即可运用罗尔定理证明存在ξ∈(a,b)，使得F'(ξ)=0,也就是f(ξ)=0，那么也能证明至少存在一个根
方程的根个数问题
- 运用单调性，如果函数单调，（那怎么证明函数单调，可以运用定义也可以一阶导看正负）且函数有根，那么有且只有一个根。
- 运用罗尔定理的推论

复习全书基础篇P46例13，先用零点定理证明根存在，这道题中巧妙地运用导极限思想，x趋向于负无穷的时候函数值趋向于负无穷，x趋向于正无穷的时候函数值趋向于正无穷，那么说明存在a<b，使得两端点异号。然后再用函数单调性，这里使用求导看一阶导数的正负来证明根的个数问题
复习全书基础篇P47例14，这道题要求证明至少有一个实根，即证明根的存在性问题，使用零点定理或者罗尔定理。在尝试使用零点定理时并不能判断两端点的正负号故使用罗尔定理。找到一个函数求导之后等于题目原函数，再利用罗尔定理条件证明存在即可。

证明函数不等式的常用方法有三种：

复习全书基础篇P47例18，先分别在[a,c]和[c,b]区间上用罗尔定理得到两个一阶导相同的两个ξ值，再对这两个ξ用罗尔定理就可得到二阶导的结果为0的结果，其实就是罗尔定理的深刻理解。
复习全书基础篇P47例19，复习全书基础篇P47例20。这两题用的一个非常重要的思想就是f'(ξ)在什么情况下大于0或者小于0，结合几何意义理解就是斜率的正负，那么只要找好相应区间即可。
复习全书基础篇P47例21，第一问用介值定理即可做出；第二问可以使用拉格朗日定理但是更普遍的是会使用构造辅助函数然后用罗尔定理，即找到某F(x)，使F'(x)等于题目中所给到的函数然后利用罗尔定理即可。