目录
前言
目前的研究方向还是以 HSIC (HyperSpectral Image Classificaition) 为主了。开始整理看过的论文，第一篇就从 HybridSN 开始。
HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification
S. K. Roy, G. Krishna, S. R. Dubey and B. B. Chaudhuri, "HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification," in IEEE Geoscience and Remote Sensing Letters, vol. 17, no. 2, pp. 277-281, Feb. 2020, doi: 10.1109/LGRS.2019.2918719.
- The source code can be found at https://github.com/gokriznastic/HybridSN.
- Date of Publication: 12 June 2019
说白了 HybridSN 其实就是混合了 2D-CNN 和 3D-CNN，而之所以要混合，就是因为要“取其精华去其糟粕”。正如 Paper 中引出 HybridSN 提出动机所讲：
" The 2D-CNN alone isn’t able to extract good discriminating feature maps from the spectral dimensions. Similarly, a deep 3D-CNN is more computationally complex and alone seems to perform worse for classes having similar textures over many spectral bands."
论文思路
高光谱图像基础
尽管这篇文章没有过多地去介绍高光谱图像（HSI）的相关知识，但是作为第一篇整理的论文，还是在这里简单说一下。如果要展开来说，那有太多的基础知识去补充了，因为当初去了解的时候就是“一层一层挖”，比如：高光谱图像什么意思？这个"高"高在哪里？多光谱图像又是什么？怎么区别高光谱图像和多光谱图像？高光谱图像怎么拍出来的？.....
我们先来看一下上面这张照片，这是我在 @condifood 这个公司官网找到的图，从左到右分别是单色图像（也就是我们常说的灰度图像，即只含亮度信息，不含色彩信息，该图像的每个像素的 R/G/B 数值都是相同的）、彩色图像、高光谱图像。单从颜色这个角度去看，好像第三张高光谱图像也有颜色（深板岩暗蓝灰色？），实际上这是 False Color，也就是伪彩色图像，实际上严格来说第二张图片有三个通道，而第三张图片则是由上百个通道，我们看到的只是选择了三个通道进行显示所呈现出来的图像，这是我想给大家带来高光谱图像的第一印象。
第二：高光谱图像是由成像光谱仪拍的。而高光谱遥感技术即：利用成像光谱仪，在电磁波的可见光，近红外，中红外和热红外波段范围内，以纳米级光谱仪在几十个或几百个波段同时对地物进行成像，并记录地物的连续光谱响应，实现了地物空间信息，辐射信息，光谱信息的同步获取。（PS：成像光谱仪的原理就不说了，有兴趣可以自行 search）
第三：因为物体反射、吸收、透射和辐射电磁波的能力不同，所以我用着成像光谱仪（里面有不同的电磁波）去照地物表面的时候，地物会对这些电磁波有不同的反射，我就可以根据这些反射的不同去区分地表有什么不同的物质。这些反射的信息就是高光谱图像中丰富的光谱信息，在高光谱图像中的第三个维度得以体现，最后就构成了高光谱立体数据。关于立体，看下面这张图就非常清晰了。
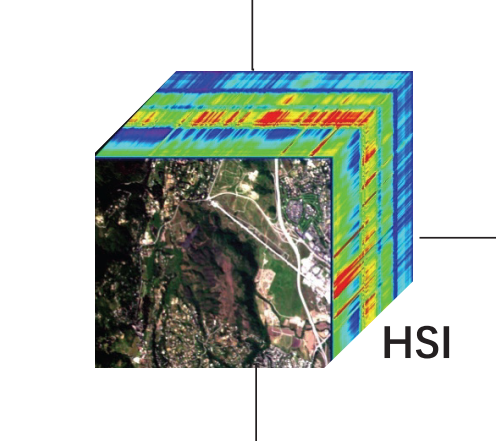
说白了，高光谱图像和我们平时看到的照片有什么不同呢？空间特征（宽、高）还是一样的，只是你所看到的颜色（在这里或者已经不能说是颜色了），更准确的来说是突破了用颜色代表波段的局限。图像的通道数已经不是普通照片的 3 个，而是几百个，我们所看到的很多高光谱图像数据集，虽然说是数据集，其实每一个数据集就是一张高光谱图像，但是里面包含的数据很丰富。
高光谱图像分类在分类什么？
经过上面的些许基础知识普及，可能又有一个疑问，数据集其实就是一张图片，那分类什么？
上面说过高光谱图像有着丰富的信息，而对应到每一个像素，也就是 $1×1×通道数$ ，这里的 $1$ 代表的是一个像素，但是不代表我探测的地表的一平方米或者一平方厘米，取决于你所使用的高光谱传感器的空间分辨率。我们所要做的就是对这个像素进行分类到相对应的地物类别。也就是说：高光谱分类其实就是对每一个像素进行分类。这个像素属于玉米？大豆？树林？最后的分类类别取决于你这个高光谱数据集在哪里拍的，那个地方有什么地物分类。
思路概括
像上面所说，HybridSN 的提出并不是凭空提出，是因为在 HybridSN 提出之前，2D-CNN 和 3D-CNN 的 Application 在高光谱图像分类中各有优点和弊端：
- 2D-CNN（二维卷积）：当然可以去提取 HSI 的空间特征（宽，高），但是对于你的光谱特征我无能为力；
- 3D-CNN（三维卷积）：可以同时提取 HSI 的空间特征和光谱特征，但是如果纯用 3D-CNN 整体计算量就大大增加（因为 HSI 的光谱通道多的吓人）
这里有个小基础知识。你可能会说 2D-CNN ，即二维卷积也就是我们平常使用到的图像卷积，也有多通道卷积啊，不能提取光谱特征吗？这里就涉及到二维卷积和三维卷积的区别：区分二维卷积或者三维卷积，看的是卷积的方向维度，二维卷积只在两个维度（高度和宽度方向）进行卷积操作，即使有多个通道，但是最后计算是叠加求和。而三维卷积能在三个维度（高度、宽度和深度方向）进行卷积操作。这意味着使用2D-CNN处理高光谱图像时，我们只能分别处理每个光谱通道的特征，并无法发现不同光谱通道之间的相关性，也就无法挖掘出所有可能的特征信息。对于3D-CNN，不会将每个光谱通道视为一个独立的图像，而是将所有通道作为一个三维体积来处理，从而能够同时捕捉图像的空间和光谱特征。使用3D-CNN处理高光谱图像更加适合，可以实现更好的分类性能。
2D-CNN 简单但是只能 capture 空间特征，3D-CNN 虽然对空、光谱特征都能 capture 到，并且能够提高分类的准确率，但是计算量上来了。
所以 HybridSN 就有提出的 Motivation，我可以结合 2D-CNN 和 3D-CNN 的优点，在 HybridSN 中，先使用三维卷积再堆叠二维卷积，最后连接分类器。这样就能很好地提取空间特征和光谱特征，计算量又不会很大。
有了基本思路，作者就具体提出 HybridSN 的网络结构（怎么混合？），然后就是实验分析，最后便是总结。
网络结构
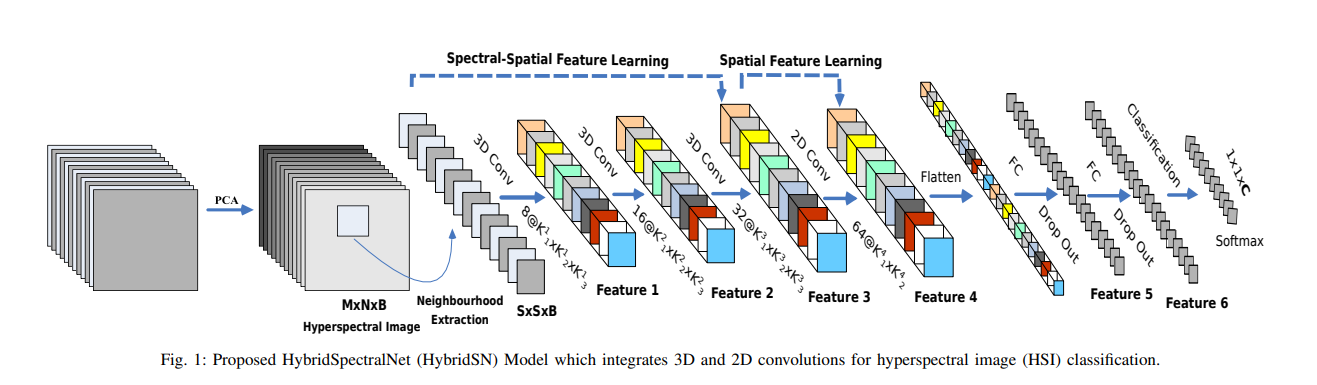
上图即为原论文中 HybridSN 的网络结构，原始高光谱立方体数据集输入，经过 PCA 降维得到空间特征相同，但是光谱通道数降为 $B$ 的立方体数据集，接着就是邻域像素提取，分割成一个个小立方体数据集。
接着就是 HybridSN 的核心部分：经过三层 3 维卷积，再经过一层 2 维卷积，2 层全连接层，1 层 SoftMax 分类层。
就拿 Indian Pines 数据集来说，原始输入为： $145×145×200$ ，首先进行 PCA 降维，降到 $145×145×30$ ，我们要对每个像素进行分类，所以要分割成每一个像素进行后续的卷积操作，可是分割成每一个像素进行卷积之后，卷着卷着之后大小就很小了，所以对原始图像每个像素点进行填充，将其封装成一个邻域像素块，接下来就是对这个邻域像素块进行卷积操作。
先不管这里面如何操作的，总之 Indian Pines 的输入，经过 PCA 降维后进行分割像素填充邻域像素块后，可以分割成：10249 个这样 $25×25×30$ 这样的小立方体，其中 25 是作者试验出来的参数，也就是说最后的小立方体宽高都是 25 个像素，30 也就是 PCA 降维之后保留的光谱维度。
初始准备工作完成（准备要卷积的小立方体块），接着就是先 3 层 三维卷积，接着就是 1 层 二维卷积，在二维卷积前，reshape 一下，堆叠其后两个维度，从而符合二维卷积的形状。接着经过二维卷积之后，进行一个 Flatten（拉平） 送入第一个全连接层，然后再送入第二个连接层，最后送入 Softmax 进行分类，因为最后 Indian Pines 最后地物分类有 16 种，所以最后一层有 16 个神经元。
实验结果
高光谱图像数据集介绍
在这篇 Paper 中，使用了高光谱图像的三个主要数据集：
- Indian Pines
- University of Pavia
- Salinas Scene
趁这个机会，我也稍微介绍一下高光谱的数据集。高光谱数据集不多，因为采集难度高（现在采集难度已经大大降低，因为发射了挺多高光谱卫星可以帮助我们更好地采集高光谱影像），标注也很麻烦（人工标注到现在也是一个主要问题，采集图像变简单了，但是标签的人工标注还是比较困难，因为需要有这方面知识的专家进行人工标注），比较经典的其实就是这篇论文所用到的三个，当然还有其它数据集。在阅读 HSIC 的论文的时候，你会发现这几个数据集出镜率非常高，基本上以后我们自己发论文也是依靠这么几个数据集。
此外要补充的一点是：高光谱分类数据集中通常有该图像的空间分辨率和光谱分辨率两个评价标准。
空间分辨率指的是图像中每个像素所代表的区域大小，即图像中最小可分辨物体的大小。比如，“20m 空间分辨率” 意味着一个像素对应地面上的 20 平方米 区域。高空间分辨率有助于检测细小的地物和更精细的分类。当然从数值角度来看，空间分辨率的数值越低，代表空间分辨率越高，比如说：“1m 空间分辨率”意味着一个像素对应地面上的 1 平方米区域比“20m 空间分辨率”要高，也就是越精细（看的越清楚）；
光谱分辨率指的是光谱中不同频段之间的分隔度，即图像中不同波段之间的分隔度。比如，一个20 nm的光谱分辨率意味着相邻两个波段之间的差异至少有 20 nm。一般情况下，光谱分辨率越高，两个相邻的波段之间的波长差就越小。因此，在同样的波段宽度下，传感器中包含的波段数量就会越多。高光谱分辨率有助于检测物体所呈现的更多的物理特性，如颜色和反射率。
然而事实上，空间分辨率和光谱分辨率不能两者兼得，也就是说空间分辨率高，光谱分辨率就会较低，相反亦然。原因是：对于一个遥感传感器系统，如果要提高其空间分辨率，需要缩小其接收单元的大小，这意味着传感器可以更细致地观察到地面细节，但无法避免接受到相同区域内多种光谱信号混杂的问题，即光谱混叠。这将导致相同的物像反射率在较低空间分辨率下可被忽略，但在较高空间分辨率下则会混合多个谱带信号，从而导致识别时的混淆。相反，如果要提高光谱分辨率，则需要使用光谱带宽更窄的传感器系统，使传感器能够识别更多的光谱特征。这意味着在同样的空间分辨率下，传感器可提供更多光谱信息以支持更明确的分类。但是，这也将导致相邻光谱带之间的相关性较大，从而增加了推断和分类复杂性。因此，在实践中，必须在使用遥感传感器系统之前权衡和优化空间分辨率和光谱分辨率的选择。这项工作通常与遥感应用的目标和特定数据集的规模相关。
如你所见，这些数据集的命名都是地名，事实也确实如此，比如说：Indian Pines。
- 数据集下载地址：Indian Pines Dataset 🔗
- Indian Pines 数据集由机载可视红外成像光谱仪（AVIRIS）在美国印第安纳州一块印度松树进行成像，然后截取尺寸为 145×145 的大小进行标注作为高光谱图像分类测试。
- AVIRIS 成像光谱仪成像波长范围为 0.4-2.5μm，是在连续的 220 个波段对地物连续成像的
- 下载完之后你会发现有三个文件：
Indian_pines.mat、Indian_pines_corrected、Indian_pines_gt。但实际上用到的会是后两个，第一个是完整的 Indian PInes 数据集，但是里面第 104-108，第 150-163 和第 220 个波段不能被水反射（换一种角度来讲就是这些波段会被水吸收，比如某片土地上可能比较潮湿，表面有比较多的水分，如果还使用这些会被水吸收的波段进行地物探测，那么被水吸收过的这些波段在原有物体上的光谱反射强度值会发生变化，从而导致最后误差的出现），因此，我们一般使用的是剔除了这 20 个波段后剩下的 200 个波段作为研究的对象。也就是说第一个文件数据集是 145 × 145 × 220，而第二个为 145 × 145 × 200，那么这里面的数值则是每个像素对于 200 个波长不同的光谱的光谱反射强度值。第三个是标注好的数据集（标签），它的 shape 为 145 × 145，在这145 × 145像素中，每个像素都有一个值，值的范围为 0 ~ 16，代表着 Indian Pines 16 种地物类别，有些像素不属于 16 种地物类别（背景像素，不参与分类），所以值为 0，这是标注人员已经标注好的，方便我们进行训练和测试。
其他数据集类似，另外我国这些年也有自己的高光谱数据集了，大家可以去搜索一下，也可以参考我粗略整理的高光谱数据集 。
下面是 HybridSN 论文中所使用的三个数据集的主要信息：
| 数据集 | 空间维度 | 光谱波段 | 地物类别数 | 空间分辨率 |
|---|---|---|---|---|
| Indian Pines(IP) | $145 \times 145$ | 200 | 16 | 20m |
| University of Pavia(UP) | $610 \times 340$ | 103 | 9 | 1.3m |
| Salinas Scene(SA) | $512 \times 217$ | 204 | 16 | 3.7m |
关于高光谱图像数据集，在这里想说的一点就是，虽然现在高光谱影像采集难度逐渐降低，但标注麻烦导致可训练样本少的缺点依旧没有改善，所以大家公认的有认可度的数据集可能来来去去就那么十个左右，换句话来说就是可能你每次用来训练测试的数据集也就是这么“十张图片”，只是这 10 张图片内容非常丰富，数据特别大。此外有些数据集是用不同的成像仪去拍摄，拍摄的场景也不一样，所以地物类别也不一样，图像尺寸也不一样，光谱通道数也不一样。
评价指标
使用 OA、AA、KA 来判断高光谱分类算法的性能。
- Overal Accuracy(OA)：正确分类的样本个数占总测试样本数的比例；
- Average Accuracy(AA)：各类准确率的均值；
- Kappa：用来判定结果的一致性，即预测的结果是否与真实的结果一致，其值越高表明一致性越好；
分类结果分析
作者使用提出的 HybridSN 与其他比较经典的高光谱图像分类方法作比较（包括机器学习方法与深度学习方法），有：SVM、2D-CNN、3D-CNN、M3D-CNN、SSRN。实验结果如下（来自论文中的图片）;
这是作者对结果的分析：
“Table II shows the results in terms of the OA, AA and Kappa coefficient for different methods. It can be observed from Table II that the HybridSN outperforms all the compared methods over each dataset while maintaining the minimum standard deviation. The proposed HybridSN is based on the hierarchical representation of spectral-spatial 3D CNN followed by a spatial 2D CNN, which are complementary to each other. It is also observed from these results that the performance of 3D-CNN is poor than 2D CNN over Salinas Scene dataset. To the best of the our knowledge, this is probably due to the presence of two classes in the Salinas dataset (namely Grapes-untrained and Vinyard-untrained) which have very similar textures over most spectral bands. Hence, due to the increased redundancy among the spectral bands, the 2D-CNN outperforms the 3D-CNN over Salinas Scene dataset. Moreover, the performance of SSRN and HybridSN is always far better than M3D-CNN. It is evident that 3D or 2D convolution alone is not able to represent the highly discriminative feature compared to hybrid 3D and 2D convolutions”
整体来说有这么几点：
- HybridSN 在三个数据集上的表现优于其他分类方法（其次就是 SSRN 了），并且保持最小的标准差，另外可以看到 HybridSN 在 Salinas Scene 数据集中上三个评价指标达到了 100%（离谱！）；
- 并不是说 3D-CNN 就比 2D-CNN 好，这一点在 Salina Scene 数据集上有所表现：可以看到 2D-CNN 方法在 Salina Scene 数据集中表现得更好。造成这样的原因是虽然高光谱数据集如果考虑光谱特征整体分类效果会更加，但是 Salina Scene 数据集中有两个类的样本（Grapes-untrained and Vinyard-untrained）在大多数波段上有非常相似的纹理特征，而这两个类的样本数在总体可用样本数中又占比较大，所以 3D-CNN 在提取光谱特征的时候可能导致了信息冗余；
- 此外，作者拿 SSRN 和 HybridSN 结果与 M3D-CNN 作对比，更加证明了作者提出 HybridSN 的动机，单独使用二维卷积或者三维卷积，还不如混合两者：Mixing is better than using alone.
其他实验
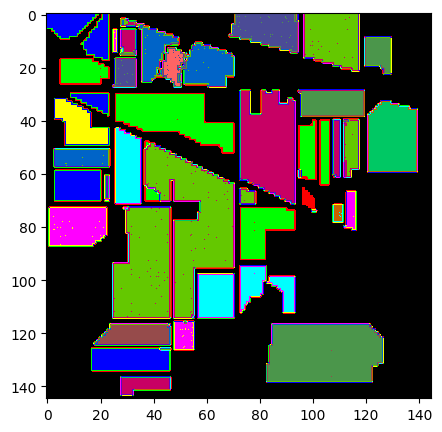
👉 而在可视化分类效果这一部分，作者对比了 HybridSN 和其他方法的分类 Map
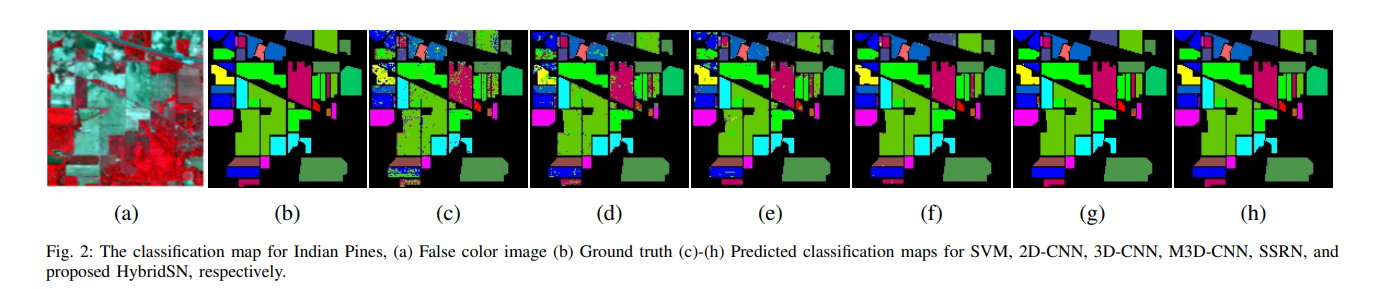
可以看出最后分类效果最佳的还是 SSRN 和 HybridSN，并且作者说在某些小部分 HybridSN 分类显示效果比 SSRN 更好。我们拿真实标签值与 SSRN 和 HybridSN 的 classification map 来看看有什么区别：
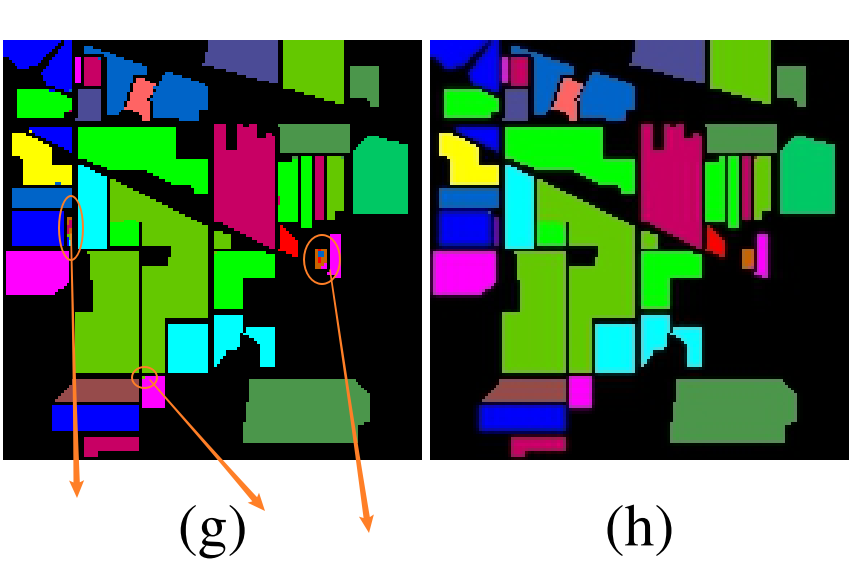
如作者所说，SSRN在某些像素分类上没有 HybridSN 强（如上图箭头所指区域像素所示等），但是总体情况上确实是不相上下。
👉 在分析 HybridSN 在 Indian Pines 数据集上训练过程中 100 个 epoch 的 Accuracy 和 Loss ，给出了如下变化曲线：
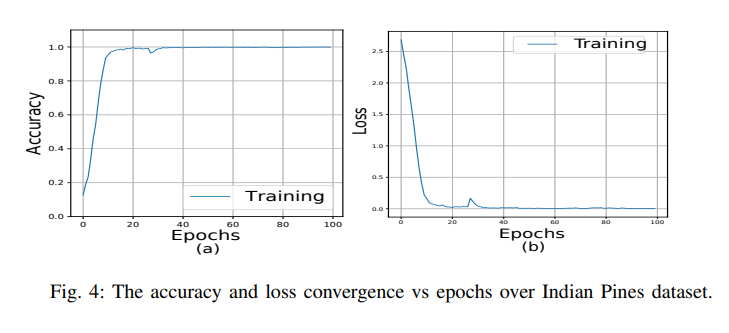
收敛大概是在 50 个 epoch 内实现的，从而表现出了 HybridSN 的快速收敛能力。
👉 在探讨 HybridSN 的计算效率上，作者对比 HybridSN 与其他分类方法的训练和测试时间：
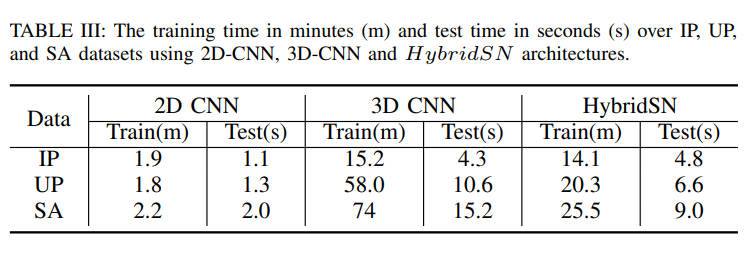
作者想表达的是混合了 2D-CNN 和 3D-CNN 的 HybridSN 计算效率是比单独使用 3D-CNN 要快的，当然肯定是说比单独使用 2D-CNN 是要慢的（毕竟多了一个维度），这也证明了作者提出的 HybridSN 的效率可行性。
👉 在分割大立方体得到小立方体的时候，作者对像素进行了邻域填充分割，而这个邻域尺寸并不是说凭空得出是：patchSize=25，作者是提出了几个尺寸然后做实验得出最佳尺寸是 25，如下图所示：
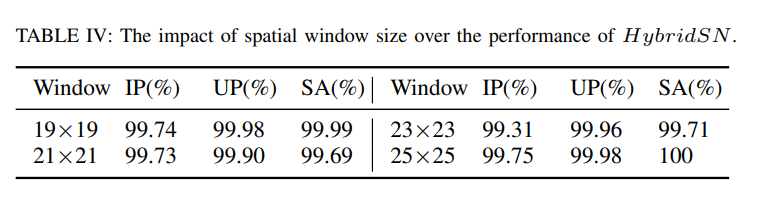
虽然有些尺寸不是 25 的 Window Size 在某些数据集上的表现的比 Window Size 为 25 的要好，但是总体来说，Window Size 为 25 是最适合 HybridSN 的。
👉 在考虑使用更少的训练数据下（仅使用了总样本的 10% ）：
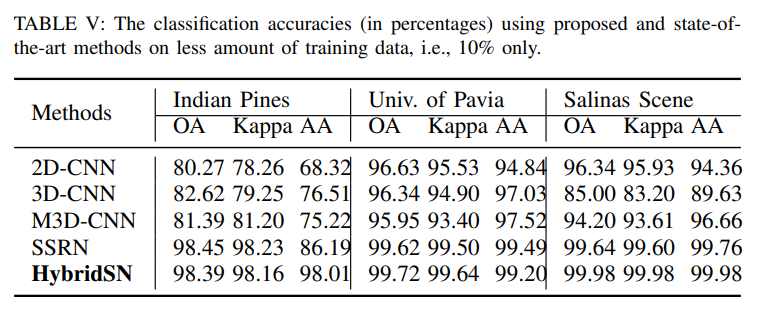
其实仔细看可以发现，在使用了更少的训练数据下，SSRN 在 Indian Pines 的 OA 竟然比 HybridSN 高，在其他数据集上也有一些指标会比 HybridSN 要高，这就有点意思了。这其实归功于 SSRN 的 residual block，我们在整理 SSRN 这篇论文的时候详细说说。
代码复现
作者提供的代码使用 Tensorflow 实现的，这里使用 Pytorch 进行复现。
导入库
import numpy as np
import scipy.io as sio
import spectral
from sklearn.decomposition import PCA
from sklearn.metrics import classification_report, accuracy_score, confusion_matrix, cohen_kappa_score
from sklearn.model_selection import train_test_split
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from operator import truediv
HybridSN 模型定义
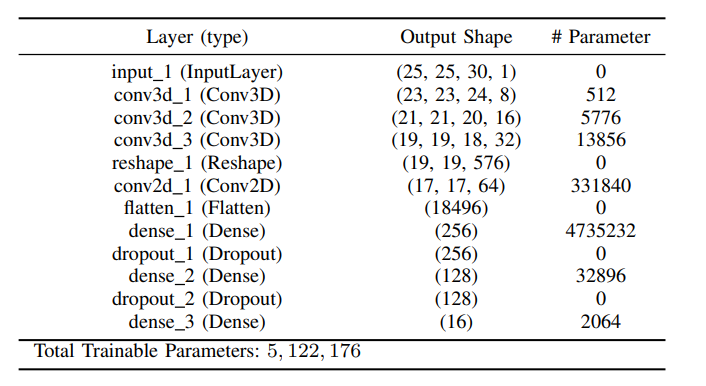
首先就是对整个模型的定义，这部分代码非常清晰，在这边直接给出，不再过多赘述。Pytorch 比较麻烦的是你要知道每层卷积之后的具体计算，这里也不再过多计算，顺便贴上论文中作者给出的每一层的 Output Shape，方便查看
# 3 层 三维卷积，一层二维卷积，三层全连接层
class HybridSN(nn.Module):
def __init__(self, num_classes=16):
super(HybridSN, self).__init__()
# 第一层三维卷积：Conv3d_1, Input:(1, 30, 25, 25), 8 个 7 × 3 × 3 的卷积核
# Output: (8, 24, 23, 23)
self.conv1 = nn.Sequential(
nn.Conv3d(1, 8, (7, 3, 3)),
nn.ReLU()
)
# 第二层三维卷积：Conv3d_2，Input:(8, 24, 23, 23)，16 个 5 × 3 × 3 的卷积核
# Output: (16, 20, 21, 21)
self.conv2 = nn.Sequential(
nn.Conv3d(8, 16, (5, 3, 3)),
nn.ReLU(inplace=True)
)
# 第三层三维卷积：Conv3d_3, Input(16, 20, 21, 21)，32 个 3 × 3 × 3 的卷积核
# Output: (32, 18, 19, 19)
self.conv3 = nn.Sequential(
nn.Conv3d(16, 32, (3, 3, 3), stride=1, padding=0),
nn.ReLU(inplace=True)
)
# 第四层是二维卷积，但是要二维卷积之前就要把第三层的输出 reshape 成可以二维卷积的形状
# 其实就是样本数和维度数堆叠：32 × 18 = 576，所以这一层二维卷积的输入为 576
# Output: (64, 17, 17)
self.conv4_2d = nn.Sequential(
nn.Conv2d(574, 64, (3, 3)),
nn.ReLU(inplace=True)
)
# 二维卷积层之后就是一个全连接层，而在送入这个全连接层之前，要把二维卷积之后的输出降为一维才能送入全连接层
# 所以在 forward 里直接使用 flatten()，那么输入全连接层参数即为：64 × 17 × 17 = 18496
# 这一全连接层有 256 个节点
self.dense1 = nn.Linear(18496, 256)
# 接着又是一个全连接层，有 128 个节点
self.dense2 = nn.Linear(256, 128)
# 最终输出层，有 num_classes 这么多节点，因为我们最后就是要分 num_classes 这么多地物类别（Indian Pines）数据集
self.dense_out = nn.Linear(128, num_classes)
# 论文中使用了 Dropout ，参数为 0.4
self.drop = nn.Dropout(0.4)
# 定义前向传播函数
def forward(self, x):
out = self.conv1(x) # 第一层三维卷积
out = self.conv2(out) # 第二层三维卷积
out = self.conv3(out) # 第三层三维卷积
out = self.conv4_2d(out.reshape(out.shape[0], -1, 19, 19)) # 第四层二维卷积
out = out.reshape(out.shape[0], -1)
out = F.relu(self.dropout(self.dense1(out)))
out = F.relu(self.dropout(self.dense2(out)))
out - self.dense_out(out)
return out
数据预处理
上面说过高光谱原始数据集是一个大立方体，我们要对其中每个像素值进行分类，所以要切割成一个个小的立方体。当然，如果按照 $1×1$ 的像素去切割的话，经过卷积之后就“所剩无几”了，所以我们选择邻域像素提取成一个个小立方体。
具体步骤是：
- 原始输入：$145 \times 145 \times 200$
- 经过 PCA 降维：$145 \times 145 \times 30$
- 邻域提取切割前，为边缘像素 padding：$169 \times 169 \times 30$
- 每个像素周围提取 patch 的尺寸为 25，结果就是 21025 个 $25 \times 25 \times 30$ 这样的小立方体
- 但是这些小立方体中有些像素不属于 16 种类别中的一个类别（背景像素），我们要 removeZeroLabels ，把这些无用数据丢弃
- 最后剩下：10245 个 $25 \times 25 \times 30$ 这样的小立方体（有效像素）
- 开始随机划分训练集和测试集：随机划分的比例为测试集占总数据集的 90%，而训练集占 10%
- 最后随机划分后的训练集和测试集按照正确的训练格式进行 transpose
上面的预处理已经说的非常详细了，下面的代码我也写上了非常详细的注释：
# 对高光谱数据集 X 应用 PCA 变换
def applyPCA(X, num_components):
newX = np.reshape(X, (-1, X.shape[2]))
# print(type(newX))
# print(newX.shape) # (145*145=21025, 200)
pca = PCA(n_components=num_components, whiten=True)
newX = pca.fit_transform(newX)
# print(newX.shape) # (21025, 30)
newX = np.reshape(newX, (X.shape[0], X.shape[1], num_components))
# print(newX.shape)
# print("------")
return newX
# 对单个像素周围提取 patch 时，边缘像素就无法取了，因此，给这部分像素进行 padding 操作
# 经过 padWithZeros 之后，宽、高会变成 169,169， 也就是左右各 padding 了 12
def padWithZeros(X, margin=12):
# print(X)
newX = np.zeros((X.shape[0] + 2 * margin, X.shape[1] + 2 * margin, X.shape[2]))
#print(newX.shape) # (169, 169, 30) 全是 0
x_offset = margin
y_offset = margin
newX[x_offset:X.shape[0] + x_offset, y_offset:X.shape[1] + y_offset, :] = X
return newX
# 对单个像素周围提取 patch 时，边缘像素就无法取了，因此，给这部分像素进行 padding 操作
def createImageCubes(X, y, windowSize=5, removeZeroLabels=True):
# 给 X 做 padding
margin = int((windowSize - 1) / 2) # 12
zeroPaddedX = padWithZeros(X, margin=margin) # (169, 30, 30)
# split patches
patchesData = np.zeros((X.shape[0] * X.shape[1], windowSize, windowSize, X.shape[2]))
# print(patchesData.shape) # (21025, 25, 25, 200)
patchesLabels = np.zeros((X.shape[0] * X.shape[1]))
# print(patchesLabels.shape) # (21025, )
patchIndex = 0
for r in range(margin, zeroPaddedX.shape[0] - margin): # for r in range(12, 169-12)
for c in range(margin, zeroPaddedX.shape[1] - margin): # for c in range(12, 169-12)
patch = zeroPaddedX[r - margin:r + margin + 1, c - margin:c + margin + 1]
# print(patch.shape)
# zeroPaddedX[r - 12 : r + 12 + 1, c -12 : c + 12 + 1]
patchesData[patchIndex, :, :, :] = patch
patchesLabels[patchIndex] = y[r - margin, c - margin]
patchIndex = patchIndex + 1
# 如果没有 removeZeroLabels
# patchesData 的 shape 将会是 (21025, 25, 25, 30)
# patchesLabels 的 shape 将会是 (21025, )
# removeZeroLabels 的作用就是去掉 gt 标签集 groundtruth 中为 0 的数据，因为里面的数据值有 0~16，而刚好 1~16 刚好对应地物分类的 16 类
if removeZeroLabels:
patchesData = patchesData[patchesLabels > 0, :, :, :]
patchesLabels = patchesLabels[patchesLabels > 0]
patchesLabels -= 1
return patchesData, patchesLabels
# 随机划分训练集和测试集
# 这里最后取 testradio=0.9 也就是随机抽 90% 为测试集，10% 为训练集
def splitTrainTestSet(X, y, testRatio, randomState=345):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=testRatio, random_state=randomState, stratify=y)
return X_train, X_test, y_train, y_test
构建训练集和测试集加载类
上面已经成功划分了训练集和测试集，但是不能直接拿来训练，因为他是不可迭代的，所以我们在下面创建可以迭代的训练集和测试集类
# 构建训练数据集
""" Training dataset"""
class TrainDS(torch.utils.data.Dataset):
def __init__(self):
self.len = Xtrain.shape[0]
self.x_data = torch.FloatTensor(Xtrain)
self.y_data = torch.LongTensor(ytrain)
def __getitem__(self, index):
# 根据索引返回数据和对应的标签
return self.x_data[index], self.y_data[index]
def __len__(self):
# 返回文件数据的数目
return self.len
# 构建测试数据集
""" Testing dataset"""
class TestDS(torch.utils.data.Dataset):
def __init__(self):
self.len = Xtest.shape[0]
self.x_data = torch.FloatTensor(Xtest)
self.y_data = torch.LongTensor(ytest)
def __getitem__(self, index):
# 根据索引返回数据和对应的标签
return self.x_data[index], self.y_data[index]
def __len__(self):
# 返回文件数据的数目
return self.len
# 创建 trainloader 和 testloader
trainset = TrainDS()
testset = TestDS()
train_loader = torch.utils.data.DataLoader(dataset=trainset, batch_size=128, shuffle=True, num_workers=2)
test_loader = torch.utils.data.DataLoader(dataset=testset, batch_size=128, shuffle=False, num_workers=2)
训练过程
# 选择 GPU 进行训练
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 网络放到GPU上
net = HybridSN().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)
# 开始训练
total_loss = 0
# net.train()
for epoch in range(100):
for i, (inputs, labels) in enumerate(train_loader):
inputs = inputs.to(device)
labels = labels.to(device)
# 优化器梯度归零
optimizer.zero_grad()
# 正向传播 + 反向传播 + 优化
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
total_loss += loss.item()
print('[Epoch: %d] [loss avg: %.4f] [current loss: %.4f]' % (epoch + 1, total_loss / (epoch + 1), loss.item()))
print('Finished Training')
测试过程
# 模型测试 (添加 net.eval())
net.eval()
count = 0
for inputs, _ in test_loader:
inputs = inputs.to(device)
outputs = net(inputs)
outputs = np.argmax(outputs.detach().cpu().numpy(), axis=1)
if count == 0:
y_pred_test = outputs
count = 1
else:
y_pred_test = np.concatenate( (y_pred_test, outputs))
# 生成分类报告
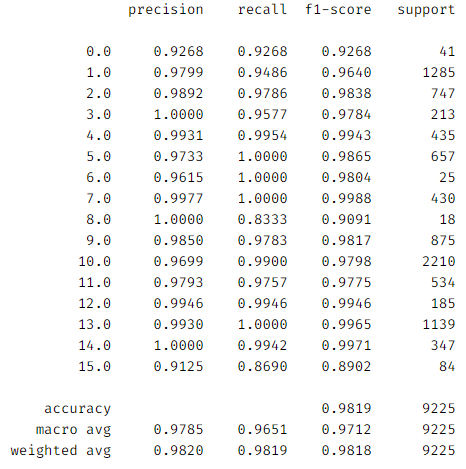
classification = classification_report(ytest, y_pred_test, digits=4)
print(classification)
之前每次测试的时候结果都不一样，其实应该要在测试之前添加 net.eval() 进入测试模式，为什么会有这个影响呢？因为在全连接层中我们使用了 Dropout 随机丢弃神经元，如果测试模式中不添加 net.eval() 那么这个随机丢弃也会继续随机，相反加入了 net.eval() 之后可以固定住训练完的 Dropout 那么分类后的结果也是一样了。
可视化分类结果
def AA_andEachClassAccuracy(confusion_matrix):
counter = confusion_matrix.shape[0]
list_diag = np.diag(confusion_matrix)
list_raw_sum = np.sum(confusion_matrix, axis=1)
each_acc = np.nan_to_num(truediv(list_diag, list_raw_sum))
average_acc = np.mean(each_acc)
return each_acc, average_acc
def reports(test_loader, y_test, name):
count = 0
# 模型测试
for inputs, _ in test_loader:
inputs = inputs.to(device)
outputs = net(inputs)
outputs = np.argmax(outputs.detach().cpu().numpy(), axis=1)
if count == 0:
y_pred = outputs
count = 1
else:
y_pred = np.concatenate((y_pred, outputs))
if name == 'IP':
target_names = ['Alfalfa', 'Corn-notill', 'Corn-mintill', 'Corn'
, 'Grass-pasture', 'Grass-trees', 'Grass-pasture-mowed',
'Hay-windrowed', 'Oats', 'Soybean-notill', 'Soybean-mintill',
'Soybean-clean', 'Wheat', 'Woods', 'Buildings-Grass-Trees-Drives',
'Stone-Steel-Towers']
elif name == 'SA':
target_names = ['Brocoli_green_weeds_1', 'Brocoli_green_weeds_2', 'Fallow', 'Fallow_rough_plow', 'Fallow_smooth',
'Stubble', 'Celery', 'Grapes_untrained', 'Soil_vinyard_develop', 'Corn_senesced_green_weeds',
'Lettuce_romaine_4wk', 'Lettuce_romaine_5wk', 'Lettuce_romaine_6wk', 'Lettuce_romaine_7wk',
'Vinyard_untrained', 'Vinyard_vertical_trellis']
elif name == 'PU':
target_names = ['Asphalt', 'Meadows', 'Gravel', 'Trees', 'Painted metal sheets', 'Bare Soil', 'Bitumen',
'Self-Blocking Bricks', 'Shadows']
classification = classification_report(y_test, y_pred, target_names=target_names)
oa = accuracy_score(y_test, y_pred)
confusion = confusion_matrix(y_test, y_pred)
each_acc, aa = AA_andEachClassAccuracy(confusion)
kappa = cohen_kappa_score(y_test, y_pred)
return classification, confusion, oa * 100, each_acc * 100, aa * 100, kappa * 100
classification, confusion, oa, each_acc, aa, kappa = reports(test_loader, ytest, 'IP')
classification = str(classification)
confusion = str(confusion)
file_name = "classification_report.txt"
with open(file_name, 'w') as x_file:
x_file.write('\n')
x_file.write('{} Kappa accuracy (%)'.format(kappa))
x_file.write('\n')
x_file.write('{} Overall accuracy (%)'.format(oa))
x_file.write('\n')
x_file.write('{} Average accuracy (%)'.format(aa))
x_file.write('\n')
x_file.write('\n')
x_file.write('{}'.format(classification))
x_file.write('\n')
x_file.write('{}'.format(confusion))
X = sio.loadmat('Indian_pines_corrected.mat')['indian_pines_corrected']
y = sio.loadmat('Indian_pines_gt.mat')['indian_pines_gt']
height = y.shape[0]
width = y.shape[1]
X = applyPCA(X, num_components = num_components)
X = padWithZeros(X, patch_size//2)
# 逐像素预测类别
outputs = np.zeros((height,width))
for i in range(height):
for j in range(width):
if int(y[i,j]) == 0:
continue
else :
image_patch = X[i:i+patch_size, j:j+patch_size, :]
image_patch = image_patch.reshape(1,image_patch.shape[0],image_patch.shape[1], image_patch.shape[2], 1)
X_test_image = torch.FloatTensor(image_patch.transpose(0, 4, 3, 1, 2)).to(device)
prediction = net(X_test_image)
prediction = np.argmax(prediction.detach().cpu().numpy(), axis=1)
outputs[i][j] = prediction+1
if i % 20 == 0:
print('... ... row ', i, ' handling ... ...')
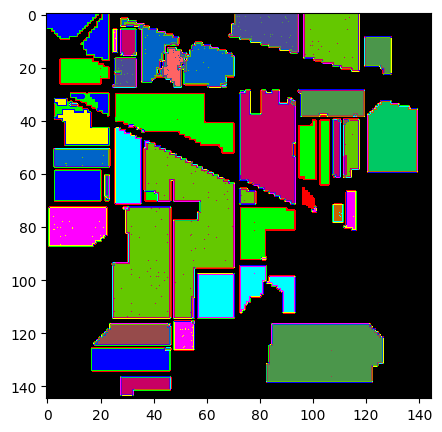
predict_image = spectral.imshow(classes = outputs.astype(int),figsize =(5,5))
HybridSN 的一些小 trick
我们再把最后分类精度的结果放上来：
尽管自己复现的时候还是与上述的结果精度相差大概一个点左右，普遍都能达到 98%+ 的分类精度，但是当初在 HSIC 刚入门的时候还是会感叹这么高的分类精度还有继续做下去的必要吗？又或者说后期推出的一些模型没有这么高的分类精度，这些论文的意义在哪里呢？
patch size
Indian Pines 数据集的尺寸是 $145 × 145$ 个像素，HybridSN 最终定好的输入卷积层的邻域像素提取的 patch 块 达到了 $25 × 25$ 个像素，这意味着什么呢？我需要用到这么大的 patch 块进行卷积才能达到这么高的分类精度，那理论上是不是输入进去的邻域像素块越大越好？那为什么不直接把 $145 × 145$ 输入进去。可是这样做 patch size 就没意义了。
这个问题在于在高光谱图像分类中，邻域像素块提取的意义在哪里？如我们所说，每个数据集的空间分辨率不一样，比如说 Indian Pines 数据集的空间分辨率为 20m，也就是说该数据集中的一个像素大小为实际地面的 $20 × 20$ 平方米那么大，在理解这个空间分辨率基础上，再考虑邻域像素提取的问题。如果邻域像素提取的越来越多，实际上在真实地面上空间信息上提取的就越来越多。这里可以算一下如果抛开 HybridSN 不谈，按照论文所说 $25 × 25$ 的 patch_size 大小为最佳，那么实际上在真实地面是提取了：$(25 × 20) × (25 × 20) $ 平方米作为一个邻域像素提取块进行特征提取，空间信息太过冗余了，如果不是 HybridSN 特有的网络，过拟合现象必定会非常严重。
一般来说，patch size 过大，增加模型的计算负担，空间冗余信息过多；patch size 过小，空间特征提取不充分。 HybridSN 根据其网络的特点将 patch size 设定在了 25，达到最后这么好的分类结果。所以你不能把其他一些不同 patch size 的方法与他作比较。此外其实 HybridSN 的采样窗口较大，会将很多样本误分类为未分类，但如果将 patch size 改小一点，HybridSN 收敛会比较差。
数据集划分
再次把代码呈现一下：
# 随机划分训练集和测试集
# 这里最后取 testradio=0.9 也就是随机抽 90% 为测试集，10% 为训练集
def splitTrainTestSet(X, y, testRatio, randomState=345):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=testRatio, random_state=randomState, stratify=y)
return X_train, X_test, y_train, y_test
上面代码中高亮的那一行中，源代码取了 345 作为随机种子，这个 345 只是随机定义的，但是一旦指定了 345，就代表这个状态是可被复现的，即作者使用 345 最后得出来的结果和我们使用 345 得出来的结果是一样的，算是保留了 345 这个随机划分的数据集最后结果。然而我们在高光谱图像分类进行实验的时候，一般会取 10 次的结果得到各项指标的标准差，然而 HybridSN 是没有体现这十次训练和测试是使用相同的数据划分亦或者是不同的数据划分，如果这 10 次结果都是使用 345 这个随机种子，那么最后的结果也是有点小 trick。
虽然我上面说的“训练样本仅使用了总样本的 10% ”，但实际上 1024 个样本算是比较多的了，如果降低样本数，HybridSN 的精度会很受影响。可以尝试现在大家常用的使用 1%，3%，5% 划分训练样本，看看最后的精度，精度就不会那么高了，在近几年（2020~2023），大家都是往小样本方向去研究 HSIC，因为它本身就是一个小样本问题，基本上最后也是划分 1%，3%，5% 这样的训练样本去测试所提出算法的性能。
其实现在很多 based on Transformer 的方法有时候还真不如 HybridSN，虽然卷积核有其固有的几何约束，但是往往高光谱图像分类所需要的特征信息并不是有多高度抽象的，而可能是稍微中高层次的特征即可。HybridSN 是一篇容易入门的文章，因为高光谱遥感图像的特殊性，使得可以用三维卷积去处理（有类似用三维卷积处理的有视频或者医学图像），可以接触到三维卷积的一些特性。并且 HybridSN 网络结构简单，就是三层三维卷积加一层二维卷积最后输入全连接层进行分类，对于新手入门很是友好了，在理解各个模块的输入输出向量维度后可以自己尝试加一些注意力或者 BatchNorm。在初 学 HSIC 代码的的时候我们更加关注的点应该是对于高光谱图像的预处理和以及特征提取。
模型改进
单独加入 BatchNorm 层
在原论文以及作者提供的代码中，在每层卷积之后（无论是三维卷积还是二维卷积）都没有 BatchNorm 层，而在深度学习中，BN 的确是奏效的，BN 层的引入可以加快收敛速度，防止“梯度弥散”，在这里就涉及到 BatchNorm 的很多基础知识，包括 BatchNorm 的原理等等，不在这里一一赘述。
在 CNN 中，BN 层引入应该要在非线性激活层之前，也就是在本代码中，应该在每层卷积中的 ReLU() 函数之前。
也就是对于 HybridSN 模型定义更改为：
# 3 层 三维卷积，一层二维卷积，三层全连接层
class HybridSN(nn.Module):
def __init__(self, num_classes=16):
super(HybridSN, self).__init__()
# 第一层三维卷积：Conv3d_1, Input:(1, 30, 25, 25), 8 个 7 × 3 × 3 的卷积核
# Output: (8, 24, 23, 23)
self.conv1 = nn.Sequential(
nn.Conv3d(1, 8, (7, 3, 3)),
nn.BatchNorm3d(8),
nn.ReLU()
)
# 第二层三维卷积：Conv3d_2，Input:(8, 24, 23, 23)，16 个 5 × 3 × 3 的卷积核
# Output: (16, 20, 21, 21)
self.conv2 = nn.Sequential(
nn.Conv3d(8, 16, (5, 3, 3)),
nn.BatchNorm3d(16),
nn.ReLU(inplace=True)
)
# 第三层三维卷积：Conv3d_3, Input(16, 20, 21, 21)，32 个 3 × 3 × 3 的卷积核
# Output: (32, 18, 19, 19)
self.conv3 = nn.Sequential(
nn.Conv3d(16, 32, (3, 3, 3), stride=1, padding=0),
nn.BatchNorm3d(32),
nn.ReLU(inplace=True)
)
# 第四层是二维卷积，但是要二维卷积之前就要把第三层的输出 reshape 成可以二维卷积的形状
# 其实就是样本数和维度数堆叠：32 × 18 = 576，所以这一层二维卷积的输入为 576
# Output: (64, 17, 17)
self.conv4_2d = nn.Sequential(
nn.Conv2d(574, 64, (3, 3)),
nn.BatchNorm2d(64),
nn.ReLU(inplace=True)
)
# 二维卷积层之后就是一个全连接层，而在送入这个全连接层之前，要把二维卷积之后的输出降为一维才能送入全连接层
# 所以在 forward 里直接使用 flatten()，那么输入全连接层参数即为：64 × 17 × 17 = 18496
# 这一全连接层有 256 个节点
self.dense1 = nn.Linear(18496, 256)
# 接着又是一个全连接层，有 128 个节点
self.dense2 = nn.Linear(256, 128)
# 最终输出层，有 num_classes 这么多节点，因为我们最后就是要分 num_classes 这么多地物类别（Indian Pines）数据集
self.dense_out = nn.Linear(128, num_classes)
# 论文中使用了 Dropout ，参数为 0.4
self.drop = nn.Dropout(0.4)
# 定义前向传播函数
def forward(self, x):
out = self.conv1(x) # 第一层三维卷积
out = self.conv2(out) # 第二层三维卷积
out = self.conv3(out) # 第三层三维卷积
out = self.conv4_2d(out.reshape(out.shape[0], -1, 19, 19)) # 第四层二维卷积
out = out.reshape(out.shape[0], -1)
out = F.relu(self.dropout(self.dense1(out)))
out = F.relu(self.dropout(self.dense2(out)))
out - self.dense_out(out)
return out
加入 BatchNorm 之后更快收敛了：
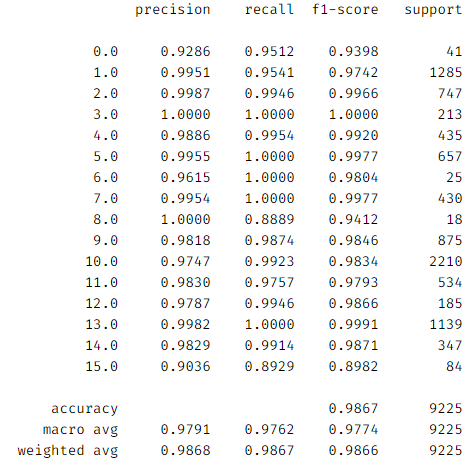
其他改进
尝试使用空间注意力机制和通道注意力机制对模型进行改进，有人复现过，得到过一点点的提升。
使用其他数据集的小问题
这是我在翻看网上关于 HybridSN 资料发现的一个问题，原链接在此：HybridSN代码修改 ， 大概意思就是说无论是作者所提供的代码还是本文章中上面所复现的代码，都是在拿 Indian Pines 数据集进行训练和测试的，可是上面的文章指出在 Pavid University 数据集上进行训练和测试的时候，内存会爆满，究其原因其实是在 patchesData 这部分出错了。我们重新拿分割大立方体的代码来看看：
# 对单个像素周围提取 patch 时，边缘像素就无法取了，因此，给这部分像素进行 padding 操作
def createImageCubes(X, y, windowSize=5, removeZeroLabels=True):
# 给 X 做 padding
margin = int((windowSize - 1) / 2) # 12
zeroPaddedX = padWithZeros(X, margin=margin) # (169, 30, 30)
# split patches
patchesData = np.zeros((X.shape[0] * X.shape[1], windowSize, windowSize, X.shape[2]))
# print(patchesData.shape) # (21025, 25, 25, 200)
patchesLabels = np.zeros((X.shape[0] * X.shape[1]))
# print(patchesLabels.shape) # (21025, )
patchIndex = 0
for r in range(margin, zeroPaddedX.shape[0] - margin): # for r in range(12, 169-12)
for c in range(margin, zeroPaddedX.shape[1] - margin): # for c in range(12, 169-12)
patch = zeroPaddedX[r - margin:r + margin + 1, c - margin:c + margin + 1]
# print(patch.shape)
# zeroPaddedX[r - 12 : r + 12 + 1, c -12 : c + 12 + 1]
patchesData[patchIndex, :, :, :] = patch
patchesLabels[patchIndex] = y[r - margin, c - margin]
patchIndex = patchIndex + 1
# 如果没有 removeZeroLabels
# patchesData 的 shape 将会是 (21025, 25, 25, 30)
# patchesLabels 的 shape 将会是 (21025, )
# removeZeroLabels 的作用就是去掉 gt 标签集 groundtruth 中为 0 的数据，因为里面的数据值有 0~16，而刚好 1~16 刚好对应地物分类的 16 类
if removeZeroLabels:
patchesData = patchesData[patchesLabels > 0, :, :, :]
patchesLabels = patchesLabels[patchesLabels > 0]
对于 patchesData 我们最先做的是初始化这么一个四维张量，并且 sample 数为 X.shape[0] * X.shape[1]，Indian Pines 的 spatial demension 是 145 × 145，没有问题；而 Pavia University 的 spatial demension 是 512×217 ，已经达到了 111104，而 Indian Pines 才 21025，这无疑为内存带来了巨大的压力。
解决的方法如上面文章里面所说，上面我们讲解代码的时候也有所提及，最后真正的 patchesData 其实并非有 21025，因为最后的 Label 不是每一个 split 出来的小立方体都是在 1~16 这个类别中，也就是 label = 0，这部分我们需要进行丢弃，即代码中的 removeZeroLabels。所以，从这个角度去思考，我们是不是可以先去看看真正有用的 label 有多少，也不是先让内存去占 height * weight 这么多空间呢？
这就是解决的方法，先对这么多个小立方体进行一个循环，找到真正有类别的小立方体，再去开辟空间，改善后的代码如下：
# 在每个像素周围提取 patch
def createImageCubes(X, y, windowSize=5, removeZeroLabels = True):
# 给 X 做 padding
margin = int((windowSize - 1) / 2)
zeroPaddedX = padWithZeros(X, margin=margin)
# 获得 y 中的标记样本数
count = 0
for r in range(0, y.shape[0]):
for c in range(0, y.shape[1]):
if y[r, c] != 0:
count = count+1
# split patches
patchesData = np.zeros([count, windowSize, windowSize, X.shape[2]])
patchesLabels = np.zeros(count)
count = 0
for r in range(margin, zeroPaddedX.shape[0] - margin):
for c in range(margin, zeroPaddedX.shape[1] - margin):
if y[r-margin, c-margin] != 0:
patch = zeroPaddedX[r - margin:r + margin + 1, c - margin:c + margin + 1]
patchesData[count, :, :, :] = patch
patchesLabels[count] = y[r-margin, c-margin]
count = count + 1
return patchesData, patchesLabels
