Table of Contents
回顾
恋词复习
- perceive v.察觉;意识到;看作;认为
- compromise v.妥协;做出让步;损害;伤害
- permeate v.散布;传播;弥漫;渗透;渗入
- affectionate adj.有感情的;慈爱的
- pragmatist n.实用主义着
GS2-C2-660-40,150~156
把660第二章的题目做完了。 回顾一下上次的点即可。
线性代数-矩阵(二)
矩阵这部分蛮多公式要记一下这里也记一下。


数据结构-树(三)
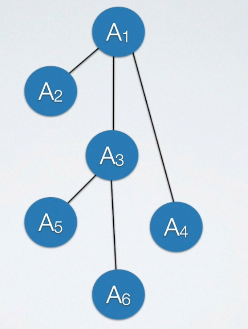
将树转换为二叉树
将树转换为二叉树的步骤如下:
- 加线。在所有兄弟结点之间加一条连线。
- 去线。对树中每个结点,只保留它与第一个孩子结点的连线,删除它与其他孩子结点之间的连线。
- 层次调整。以树的根结点为轴心,将整棵树顺时针旋转一定的角度,使之结构层次分明。注意第一个孩子是二叉树结点的左孩子,兄弟转换过来的孩子是结点的右孩子。
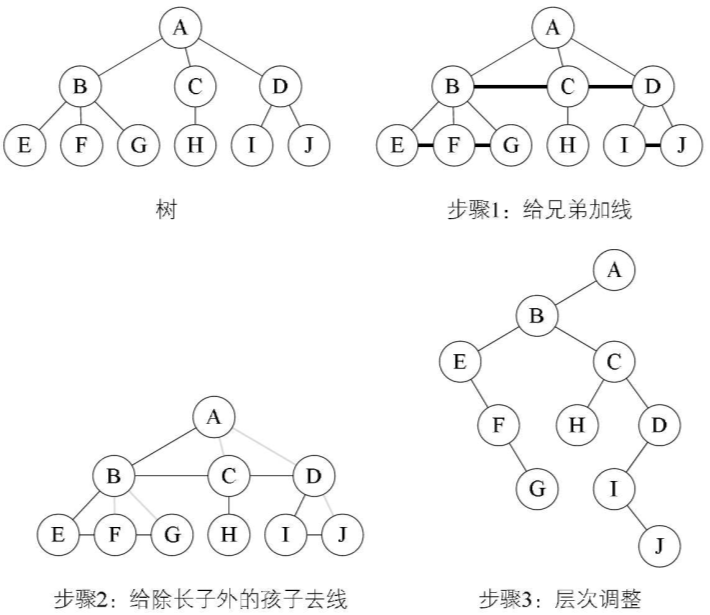
F、G本都是树结点B的孩子,是结点E的兄弟,转换后,F就是二叉树结点E的右孩子,G是二叉树结点F的右孩子
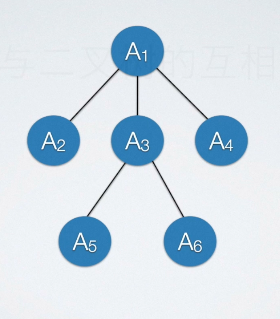
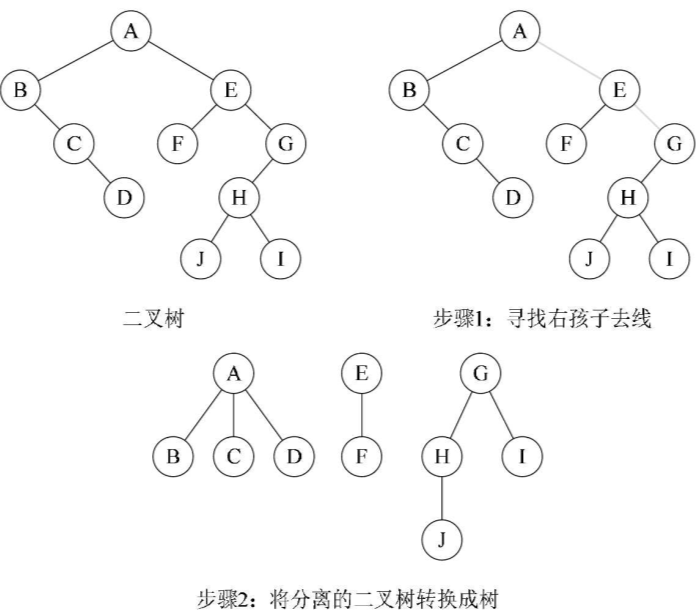
将二叉树转换为树
将之前删掉的关系补上即可。把孩子结点与父结点的所有关系都连起来,然后删除孩子结点之间的关系。
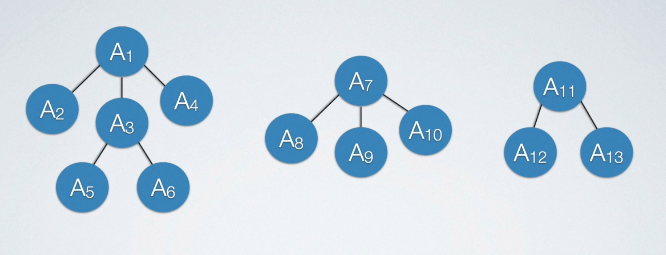
将森林转换为二叉树
森林是由若干棵树组成的,可以理解为森林中的每一棵树都是兄弟,可以按照兄弟的处理办法来操作:
- 把每个树转换为二叉树。
- 第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子,用线连接起来。当所有的二叉树连接起来后就得到了由森林转换来的二叉树
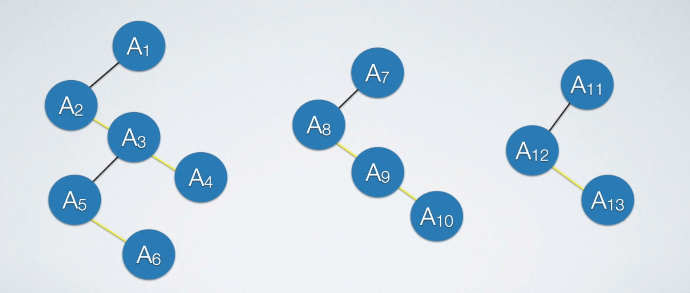
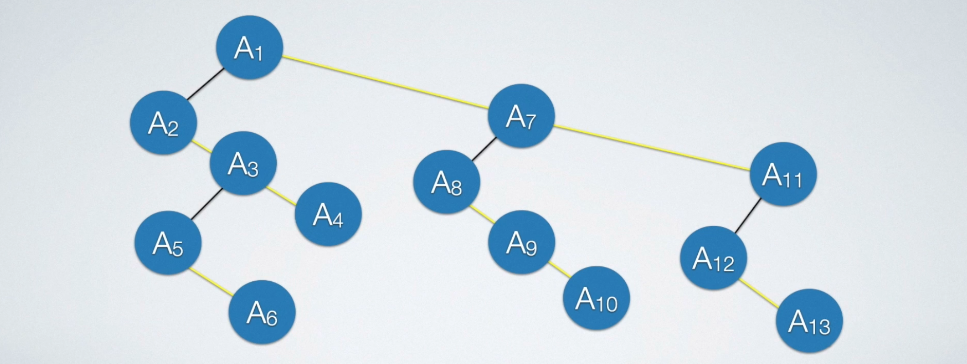
将二叉树转换为森林
判断一棵二叉树能够转换成一棵树还是森林,看这棵二叉树的根结点有没有右孩子,有就是森林,没有就是一棵树。
步骤如下:
- 从根结点开始,若右孩子存在,则把与右孩子结点的连线删除,再查看分离后的二叉树,若右孩子存在,则连线删除……,直到所有右孩子连线都删除为止,得到分离的二叉树。
- 再将每棵分离后的二叉树转换为树即可
例题

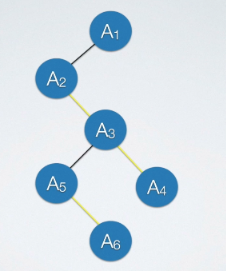
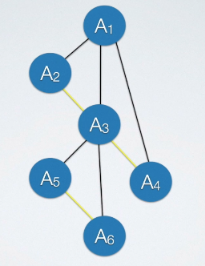
分析:由“在二叉树中,结点u是结点v的父结点的父结点”这句话可知有四种情况:
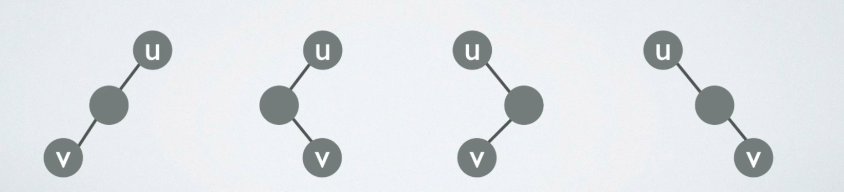
又因为题目涉及到u的父结点,可以把转换后的二叉树上把u的父结点给画出来,但是这里注意一点:这里让u作为其父结点的左孩子!如果作为右孩子,把他还原成原来的树的时候就变成u的兄弟结点了,并不是父结点所以必须是左孩子,即下图:
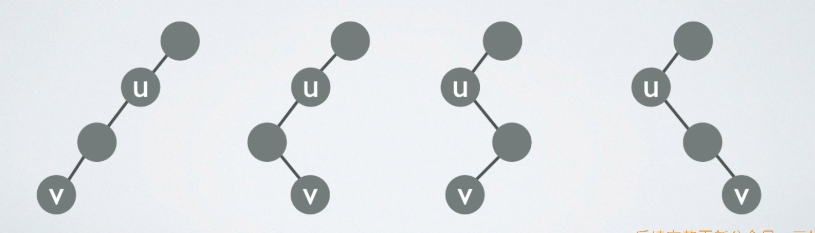
然后按照规则还原即可得到答案,只有父子或者兄弟关系,没有其他关系。