Table of Contents
回顾
恋词复习
- allege v.(未提出证据)断言
- contend v.竞争；辩论；据理力争；声称
- consent v.n 同意，赞成
- discourse n.论文；演讲；谈话 v.演讲；讲述
- idle adj.空闲的；闲置的；无用的
- resent v.对...表示愤恨
- entitle v.给予..权利；给..称号；给（书、文章等）提名
- continuous adj.连续不断的；持续的
- susceptile adj.易受感动的；过敏的
- prone adj.有..倾向的；俯卧的
- probe n. 探针；调查 v.调查；探测
线性代数-行列式
今天肝完了线性代数第一章，嗯，李永乐老师讲的还是很不错的，继续务实基础把。
行列式的概念
- 二三阶行列式
- 排列、逆序、逆序数
- n阶行列式概念
行列式的性质
按行（列）展开公式
- 代数余子式
- 展开公式
克拉默法则
看到不错的笔记，mark一下。
数据结构-矩阵（一）
考研中的矩阵
考研中对于矩阵的一些运算算法操作（转置，相加，相乘）考的很少，所以主要讲矩阵的存储。
上面这个简单的矩阵可以用int [m][n]简单搞定。
考研中矩阵又分为特殊矩阵和稀疏矩阵。相同的元素或者雩元素在矩阵中的分布存在一定规律的矩阵称之为特殊矩阵,反之称之为稀疏矩阵。
特殊矩阵 - 对称矩阵
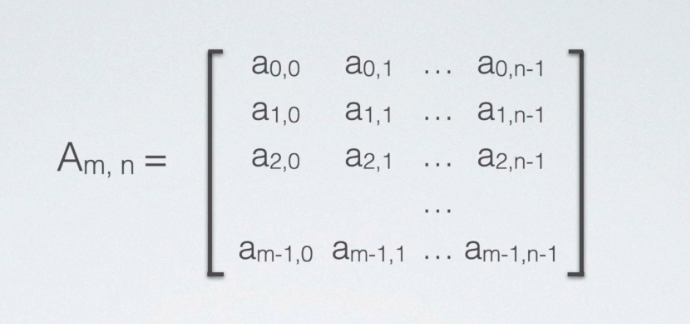
矩阵中的元素满足$a_{i,j} = a_{j,i}$的矩阵称之为对称矩阵（矩阵必须是方阵)。即以对角线为对称轴的元素相等。（ps:考研范围内只涉及主对角线对称矩阵）
例题1
分析：因为是对称矩阵，要高效，则相同元素存一份即可。可按照行优先存储方式，先存储第一行第一个，第二行，第三行，从上到下，从左至右。但题目给出的矩阵是mxn，n不是一个具体的值，一般不可能把所有的列出来的元素都给写出来，答题时一般采取存储关键位置上元素，然后其余元素可以根据这些关键位置上的元素推算出他们在一维数组中的位置，哪些元素比较重要，如图中黄色加重部分。
- 第一个元素$a_{0,0}$的下标，显然为0；
- 存取$a_{n-1,0}$时，他在数组中的位置怎么算？显然只要求出它上面的所有行中的元素即可。上面元素总和是一个首项为1，末项为n-1的等差数列的和，即
n(n-1)/2，因此$a_{n-1,0}$是n(n-1)/2+1个元素；又因为第k个元素在一维数组中的下标为k-1，所以$a_{n-1,0}$的下标为n(n-1)/2。 - 右下角元素$a_{n-1,n-1}$方法类似可算出为
n(n+1)/2-1。
例题2
$a_{i,j}$前边有i-1行零j-1个元素
由于只需要存下三角部分,所以前i-1行的元素个数为∶(1+i-1)(i-1)/2= i(i-1)/2
第i行有j-1个元素,因此$a_{i,j}$,为第i(i-1)/2+j个元素。
特殊矩阵 - 三角矩阵
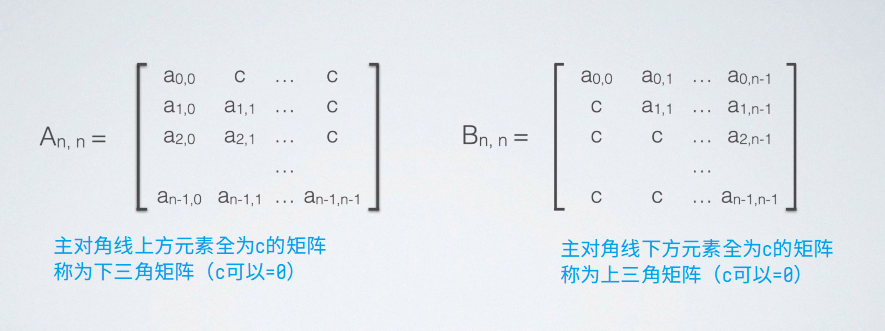
拿B作为例子，存关键元素。
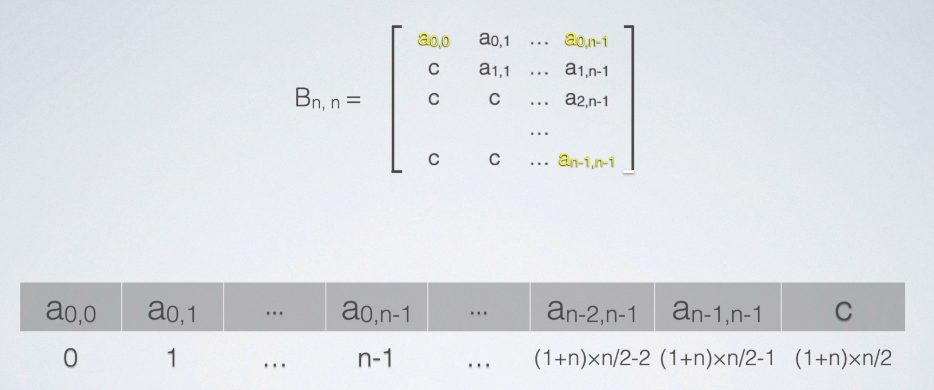
- 按照行优先存储，则数组第一个元素显然是$a_{0,0}$，然后象征性地存后面那个元素。
- 第二个关键元素为$a_{0,n-1}$，显然下标为
n-1。 - 存最后一个元素$a_{n-1,n-1}$，它上面所有行中，除去对角线及其以上元素，显然是首项为1，末项为n的等差数列的和-1个。即
n(n+1)/2 - 1，那么象征性地存它之前一个元素给表示出来。 - 这时矩阵元素还有一大堆
c没有存储，只需存一份即可，一般将c放在最后一个位置。
特殊矩阵 - 对角矩阵
矩阵中除了c之外的元素分布在对角线附近的带状区域内并且形成的这个图形是是关于对角线轴对称的。这个图形内的元素沿着对角线的方向有几行，就称之为几对角矩阵。
例题1
当i等于1时，带状区域内第一个元素为矩阵中第一个元素,其在一维数组中下标为0;
当i大于1时,第i行之前的元素个数为2+(i-2)×3，则带状区域内第一个元素X在一维数组中的下标为2+(i-2)×3。
真题
直接套用上面的公式即可：2+(30-2)x3+1=87。
