Table of Contents
回顾
恋词复习
- resort v.求助;诉诸;凭借 n.旅游胜地
- undercover adj.暗中进行的;秘密干的
- engender v.引起
--
数据结构-双端队列-栈与队列(七)
引入
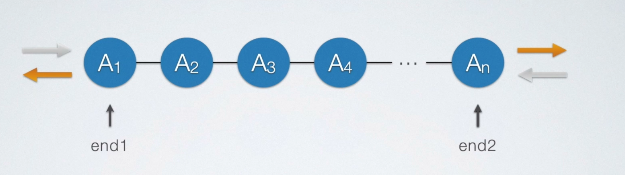
在两端都可以进行插入和删除的队列。
其实这章所讲的栈与队列都是由这种逻辑结构加了一些约束而得到的比如
- 把这个双端队列在一端进行约束,即在一端既不让它删除也不让它插入,这就为栈了。
- 把这个双端队列每一端只限制一个,即在一端限制插入,在另一端限制删除,这就为队列了。
输入受限和输出受限
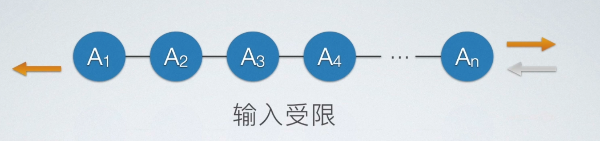
- 输入受限
在某一端限制其只能进行插入操作,而在另一端不作限制,即为输入受限的双端队列。
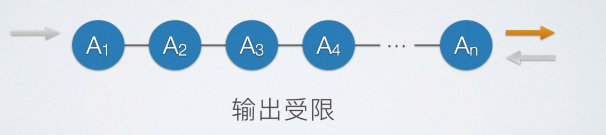
- 输出受限
在某一端限制其只能进行删除操作,而在另一端不作限制,即为输出受限的双端队列。
例题
自己动手做一遍

1)不可能通过输入受限的双端队列输出的序列是?
先假设双端队列某一端全部堵上(既不能输入也不能输出),那么栈形态下不可能的序列数即为:
4!-14=10种,然后再把这个双端序列某一端放开输出功能,接着就可以找出10种序列其中的一部分不可以的。(考研题目不会让你找这10种是什么,只会给选择给你判断。)这里列出10种分别是
1、4、2、3 //1入,1(左/右)出,2入,3入,4入,4右出,2左出,3右出。√
2、4、1、3 //1入,2入,2右出,3入,4入,4右出,1左出,3右出。√
3、4、1、2 //1入,2入,3入,3右出,4入,4右出,1左出,2右出。√
3、1、4、2 //1入,2入,3入,3右出,1左出,4入,4右出,2左出。√
3、1、2、4 //1入,2入,3入,3右出,1左出,2左出,4入,4(左/右)出。√
4、3、1、2 //1入,2入,3入,4入,4右出,3右出,1左出,2(左/右)出。√
4、1、3、2 //1入,2入,3入,4入,4右出,1左出,3右出,2(左/右)出。√
4、2、1、3 //1入,2入,3入,4入,4右出,2出不了,得不出结果。×
4、2、3、1 //1入,2入,3入,4入,4右出,2出不了,得不出结果。×
4、1、2、3 //1入,2入,3入,4入,4右出,1左出,2左出,3(左/右)出。√
2)不可能通过输出受限的双端队列输出的序列是?
同理。
1、4、2、3 //1(左/右)入,1出,2右入,3左入,4右入,4出,2出,3出。√
2、4、1、3 //1(左/右)入,2右入,2出,3左入,4右入,4出,1出,3出。√
3、4、1、2 //1(左/右1)入,2左入,3右入,3出,4右入,4出,1出,2出。√
3、1、4、2 //1(左/右)入,2左入,3右入,3出,1出,4右入,4出,2出。√
3、1、2、4 //1(左/右)入,2左入,3右入,3出,1出,2出,4(左/右)入,4出。√
4、3、1、2 //1(左/右)入,2左入,3右入,4右入,4出,3出,1出,2出。√
4、1、3、2 //1(左/右)入,2左入,3无论左入还是右入,最后都得不出结果。×
4、2、1、3 //1(左/右)入,2右入,3左入,4右入,4出,2出,1出,3出。√
4、2、3、1 //1(左/右)入,2右入,3左入,4右入,4出,2出,得不出结果。×
4、1、2、3 //1(左/右)入,2左入,3左入,4右入,4出,1出,2出,3出。
408真题


做完上面的题,这道题就更简单了。可知是一个输出受限双端队列,如右图所示。然后按照上面的方法一个个试一下即可。
(A)bacde //a左右入,b右入,b出,a出,c左右入,c出,d左右入,d出,e左右入,e出。
(B)dbace //a左右入,b右入,c左入,d右入,d出,b出,a出,c出,e左右入,e出。
(C)dbace //a左右入,b右入,c右入,d右入,d出,不行,得不出结果。
(D)ecbad //a左右入,b右入,c右入,d左入,e右入,e出,c出,b出,a出,d出。
数据结构-栈的扩展-栈与队列(八)
共享栈
假设发生左图情况,对于栈S1已经满了,而栈S2还有很多存储空间,而此时S1要存储元素多于5个,那怎么办呢?如果能把S2栈种多余空间给S1用就好了。
那么就可以如右图所示,把两个栈存储空间给合并。
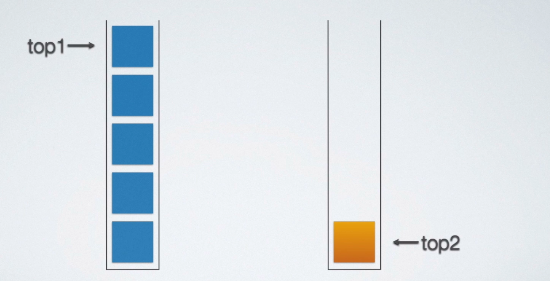

共享栈的特点
- 两个栈共享同一片存储空间。
- 这片空间不属于任何一个栈,某个栈需要得多一点,他就可能得到更多的存储空间。
共享栈结构定义与实现
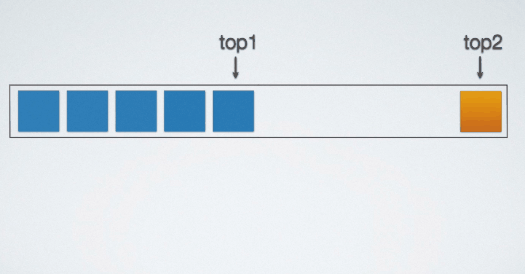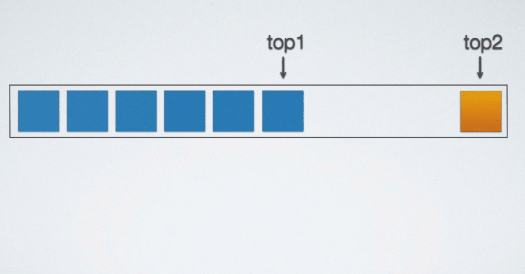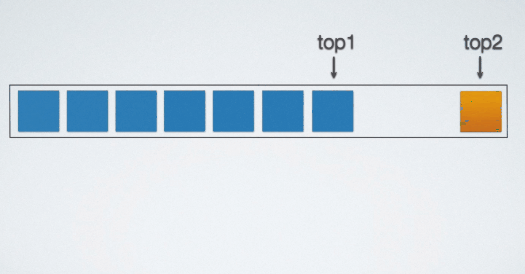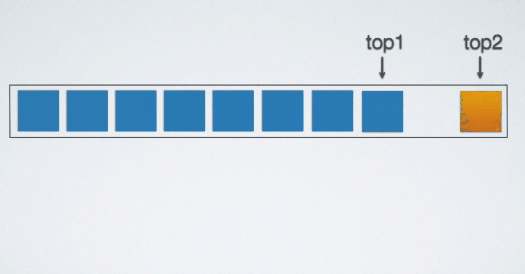

观察上图共享栈的结构,两个栈的栈底在这片存储空间的两端。当元素入栈的时候,两个栈的栈顶"指针"相向而行。
int stack[maxSize];
int top = -1,top = maxSize;
但是! 一般为了体现这两个栈顶"指针"是属于一个共享栈的,就不用两个单独的整型变量来表示它们,而是用一个长度为2的数组来表示这两个栈顶"指针"。
int stack[maxSize];
int top[2] = {-1,maxSize};
那么入栈:

- S1入栈:
stack[++top[0]) = x; - S2入栈:
stack[--top[1]] = x;
而栈满情况:
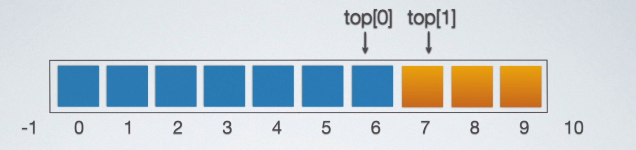
即:top[0] + 1 = top[1]。
也就是说,不存在某一个栈单独满的情况,要满,只能两个一块满,不愧是共享栈,连栈满的状态都是共享的。
用栈模拟队列
栈的逻辑特性是先进后出,而队列的逻辑特性是先进先出,那用一个栈肯定没办法模拟队列,用两个试试。
正确情况应该是这样的:
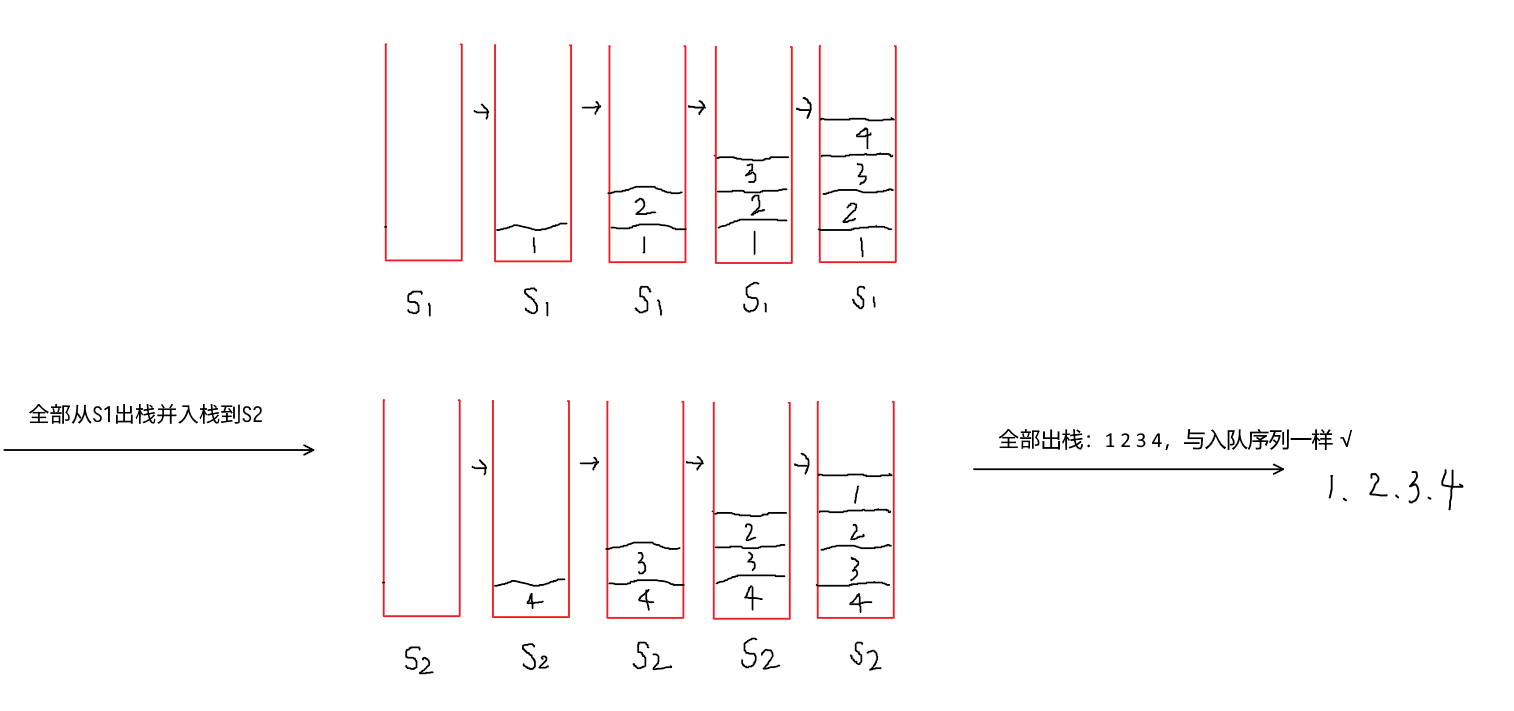
其他情况都不可以,可以自己试一下。那么就有了下面的规则:
- 入队规则
- 若S1未满,则元素直接入S1。
- 若S1满,S2空,则将S1中元素全部出栈并入S2,腾出位置再入S1。
- 出队规则
- 若S2不空,则从S2中直接出栈。
- 若S2空,则将S2中元素全部出栈并入S2,然后从S2中出栈。
队满:S1满且S2不空,则不能继续入队,即为队满状态。
队空:S1空且S2空,则队空。
数据结构-括号匹配与计算-栈与队列(九)
括号匹配
这个相关考点主要是考察在编译器中对于括号匹配技术的了解,即给定一段待编译的代码,里面涉及到很多括号,哪些括号出现的情况是匹配的,哪些括号出现的情况是不匹配的,要理解。
| 是否匹配 | 具体举例 |
|---|---|
| 匹配例子 | ()[]{},{[()]},([]).. |
| 不匹配例子 | ()[]{,)[]{},[(]).. |
可以用栈来检测。
- 初始化一个空栈,顺序读入括号。
- 若是左括号,入栈等待以后处理。
- 若是右括号,如果栈已空则不匹配,否则出栈(相当于消去一对括号)。
- 最后,栈为空则匹配,否则不匹配。
例子:{{[]}(){}[]},看动图去理解把。或者自己手画一遍更棒!

实现代码
int isMatched ( char left, char right)
{
if (left == '(' && right == ')')
return 1;
else if( left== '[' && right == ']' )
return l;
else if (left == '{' && right == '}')
return 1;
else
return 0;
}
int isParenthesesBalanced (char exp[])
{
char s[maxSize]; int top = -1;
for (int i = 0; exp[i] != '\0'; ++i)
{
if(exp [i] == '(' || exp[i] == '[' || exp[i]== '{')
s [++top] = exp [i];
if(exp [i] == ')' || exp[i] == ']' || exp[i]-= '}')
{
if(top ==-1)
return 0;
char left = s [top--];
if (isMatched (left, exp [i]) == 0)
return 0;
}
}
if(top > -l)
return 0;
return 1;
}
计算问题
考研中给出型如下图计算:
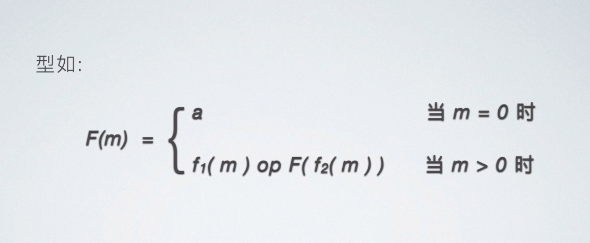
具体例子

解答
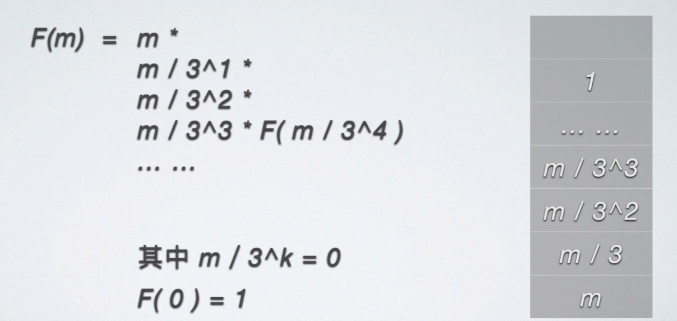
- 其实计算十分容易,一直不停的自我代入(递归),直至出现
F(0)。 - 这里做的是整数除法,即当
m<3^k时为0。 - 将每次展开的因子压入栈底。
- 其实严格来说,这里根本不需要用到栈,每次展开把得到的因式累乘即可,之所以用栈来解决,是因为这个函数的求解用递归函数求解时最清晰明了的,而递归函数则是用栈来实现的,maybe只是让我们熟悉这种思想。
int calF(int m)
{
int cum = 1;
int s[maxSize], top = -1;
while (m != 0)
{
s [++top] =m;
m /= 3;
}
while (top != -1)
cum *= s [ top--];
return cum;
}
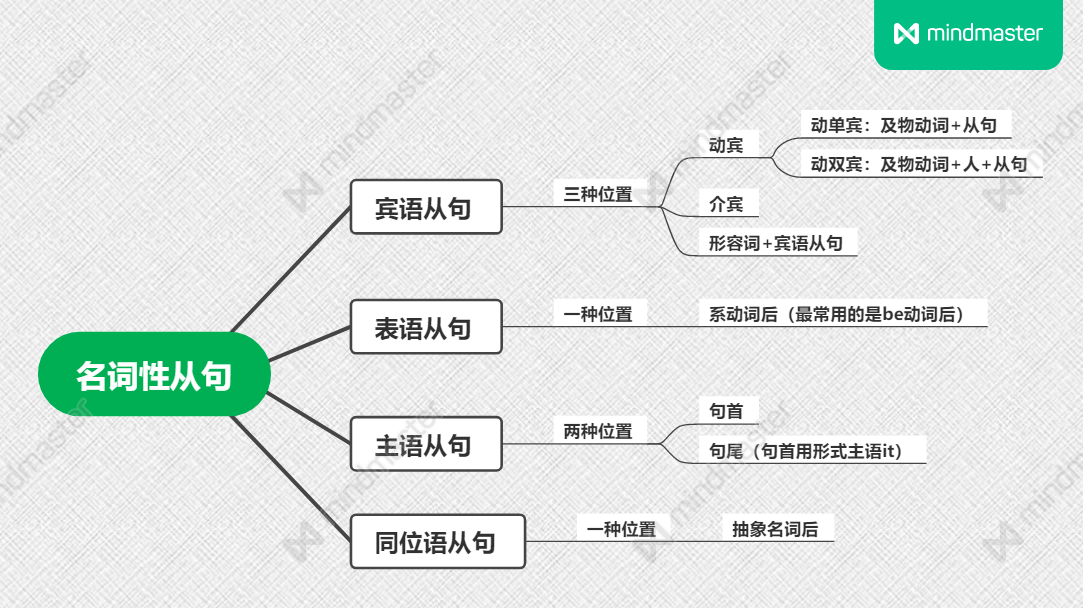
田静语法C4-S1-名词性从句