Table of Contents
回顾
恋词复习U4,U5,U6

- contend vi. 竞争;奋斗;斗争;争论 vt. 主张;为...斗争
- context n. 环境;上下文;来龙去脉;背景
- consent n. 准许,同意;赞同,同意;正式批准文件,批文;(古)一致,和谐 v. 同意,准许;(古)赞成(意见、看法等)
- content n. 内容,目录;满足;容量 adj. 满意的 vt. 使满意
无穷级数(一)- 常数项级数
级数的概念

无穷多个数的和就是用前有限项和取极限来定义的,
级数的性质

级数的申敛准则
- 正项级数


| 优点 | 缺点 | |
|---|---|---|
| 1)2) | 适用范围更广 | 不方便 |
| 3)4) | 方便 | 适用范围较小 |
- 交错级数

- 任意级数

常考题型与例题
常数项级数的敛散性判定
看笔记吧!!!!!!!!!
数据结构-数据结构-栈和队列(三)
输出序列题型1
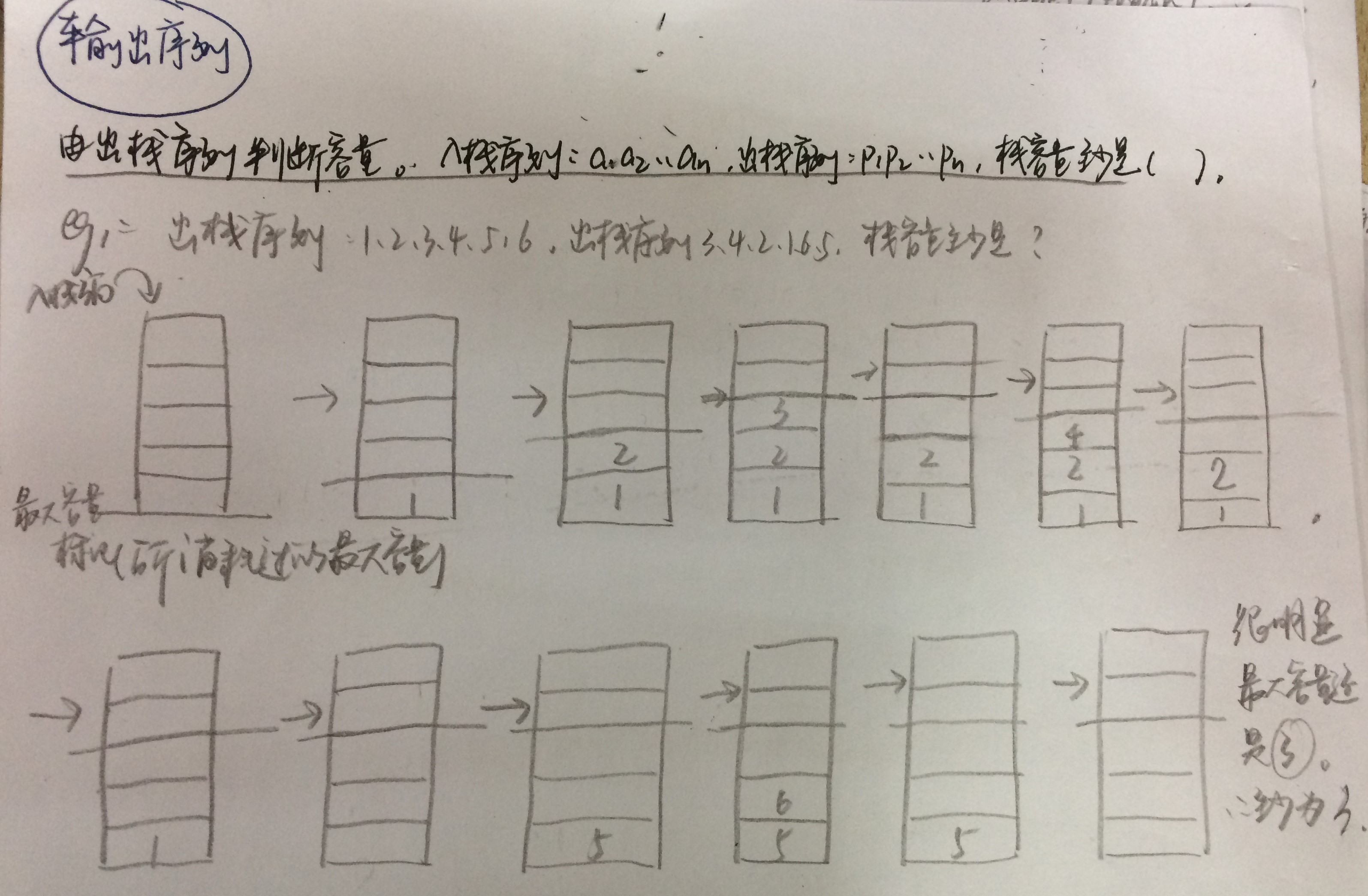
由出栈序列判断容量。入栈序列:a1a2...an,出栈序列:P1P2...Pn,栈容量至少是?




这类题都是一个做法,具体做法如下图画图理解!!下图为第一题做法,其他都是类似的,不懂看笔记!
输出序列题型2
由出栈序列判断容量。入栈序列:1,2...n,出栈序列:P1P2...Pn,若P1=n,则?
P1=n,即最后一个元素n,它第一个出栈。即在它出栈之前所有元素都已经入栈并且没有出栈,那么其出栈方式也是固定的,也就是从1到n全部入栈再出栈。
即P1=n,P2=n-1,P3=n-2,P4=n-3....Pi=n-i+1。
重要结论
若Pi=n(1≤i≤n),则 Pi>Pi+1>...Pn。(结合上题进行思考)
例题

分析:因为只需要讨论这三个元素的大小关系,只需要用穷举法,将都有可能的大小关系都列出来,看看哪些是可能的即可。

如上图:
- Pi入栈出栈,Pj入栈出栈,Pk入栈出栈,成立。
- Pi入栈出栈,Pk入栈,Pj入栈,Pj出栈,Pk出栈,成立。
- Pj入栈,Pi入栈,Pi出栈,Pj出栈,Pk入栈,Pk出栈。
- Pi最后入栈,但出栈却是第一个,即i出栈前Pj,Pk已经入栈并且没有出栈,然后Pi出栈然后只能是Pk出栈,这就与题目所给出栈序列不符合!!
- Pk入栈,Pi入栈出栈,Pj入栈出栈,Pk出栈,成立
- Pk,Pj,Pi依次入栈,然后依次出栈,成立。
由不成立的方式得出非常形象的结论:若1、2、3,则无3、1、2。

这道题等我完全搞清楚再补上,hold住。,我已经会了记录一下日期2021.4.18。
可以先假设举例:
P3 = 1,P2 = 3; //只需1入2入2出3入3出1出 √
P3 = 2,P2 = 3; //只需1入1出2入3入3出2出 √
P3 = 3;//p2都等于3了,不行 ×
P3 = 4,P2 = 3; //只需1入1出2入3入3出4出 √
//同理下面n>3都可以,所以只要P3≠3,都可以,取值个数就是n-1。
Catalan number 卡特兰数
只需记忆!!

田静语法
C1-S2-2 主语、宾语、表语的变化

主系表结构中,主语和表语都可以用非谓语动词doing或to do。但如果前后同时使用时,请注意保持前后一致,即主语和表语都使用doing,或同时使用to do.
- Seeing is believing.√
- To see is to believe.√
- Seeing is to believe.×
主语为三个对象或以上时,且都可以用and连接,那么可以省略前面的连词,换成逗号连接
- Social science disciplines include geography,economics,political science,psychology,and sociology.
需要注意的是,严格来说and之前是要写逗号的,但是考研中可以不加。
公众号更新
公众号更新了时隔两个月,刚好是2021年的第一百天!留个链接->想不出什么标题