Table of Contents
回顾
恋词U1,U2,U3,U4,U5复习
- reckon v.认为;估计;估算;指望;预计
- contend v.竞争,辩论
- fiscal adj.财政的;国库的;税收的
- lucrative adj.赚大钱的,获利多的
- preface n.序言;前言;开端;序幕
- unanimous adj.全体一致的,一致同意的
- portray v.描绘;表演;刻画
660题目回顾
好久没有回头做660,今晚决定做。我也做好心理准备很多知识点都会有点忘记了
660-P8-T16

首先是函数连续性这个知识点。在复习全书基础篇P27。关于连续性的概念,有几个定义

那么根据这道题就是f(x)在x趋向于1的极限等于f(x)在1的函数值,即 。那么回归到题本身,先要解决一个难题:
。初步判定为
e,可得 。又因为
x->+∞时,可以用无穷大量阶的比较,lnx<<x(在复习全书基础篇P13。),那么这个极限就等价于
答案
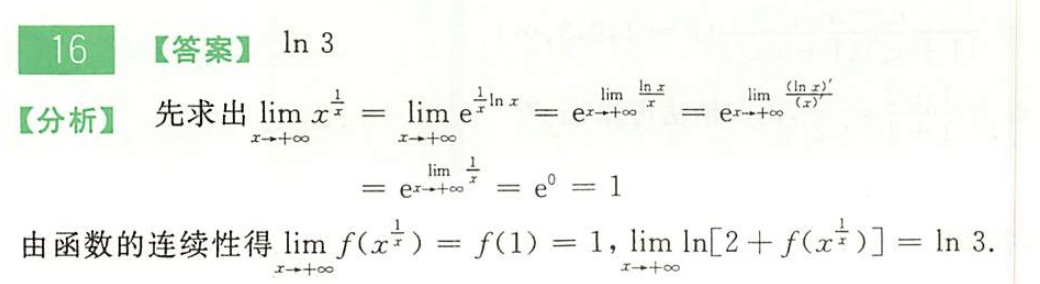
660-P8-T17
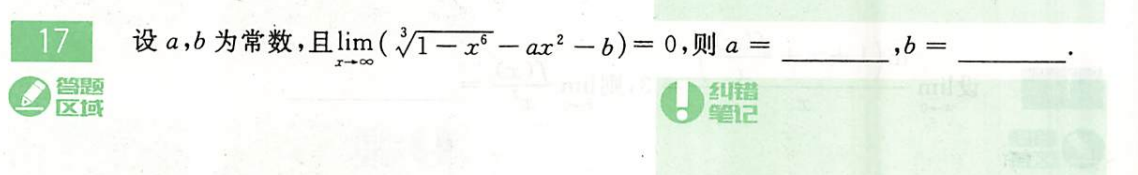
这道题不要“眼疾手快”,看到满足可以泰勒直接上泰勒公式,这里x->∞,怎么泰勒!
这种题要做多才有经验,还是要把6次方开出来,里面就能用泰勒展开,然后根据极限的性质,就可以解出a,b。
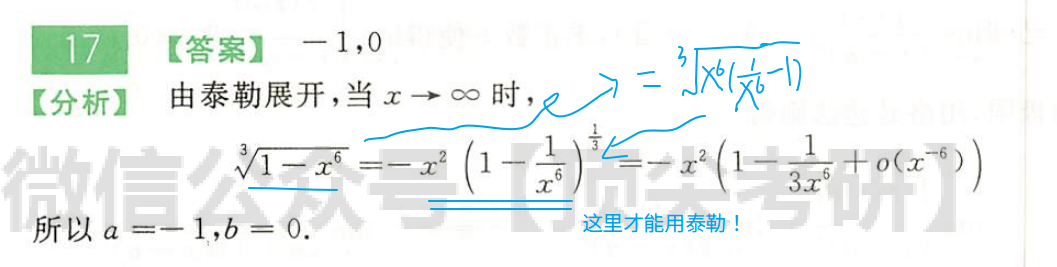
660-P8-T18
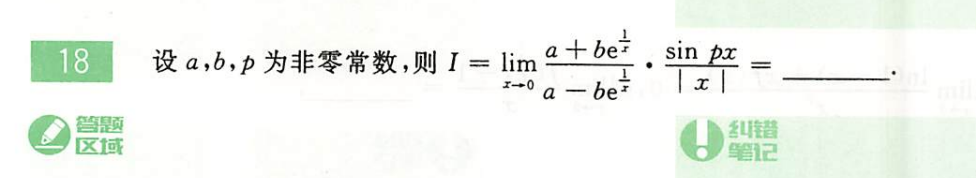
判别类型,选择方法。x->0,出现了

660-P8-T19
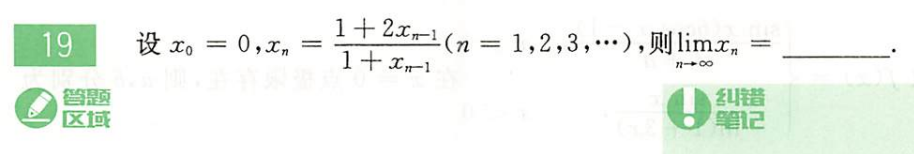
求数列极限的方法,遇到xn和xn+1的两种方法。
- 夹逼。夹逼准则比较多的是用在n项和的数列极限。
- 单调有界准则。比较多的是用在递推关系
Xn+1 = f(Xn)所定义的数列极限。单调有界准则步骤:- 用单调有界准则证明这个极限存在。
- 单调增,有上界的数列必有极限。
- 单调减,有下界的数列必有极限。
Xn+1 = f(Xn),既然极限存在了,Xn+1和Xn极限是一样的。两边取极限a=f(a),解代数方程即可。
- 用单调有界准则证明这个极限存在。

660-P8-T20

这道题要回顾的知识点是无穷小量的比较。接着根据题目列出两个等式即可做出答案。

660-P8-T21
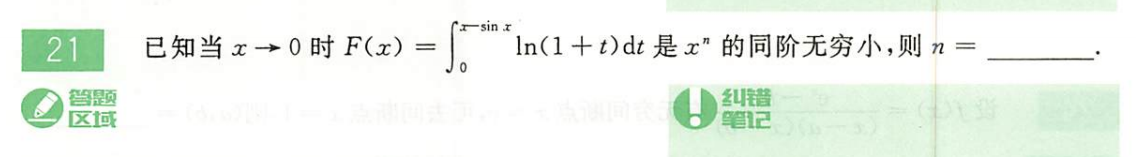
熟读题目之后整个题目就变成关于 存在的问题。那么按照求极限的过程解题即可。
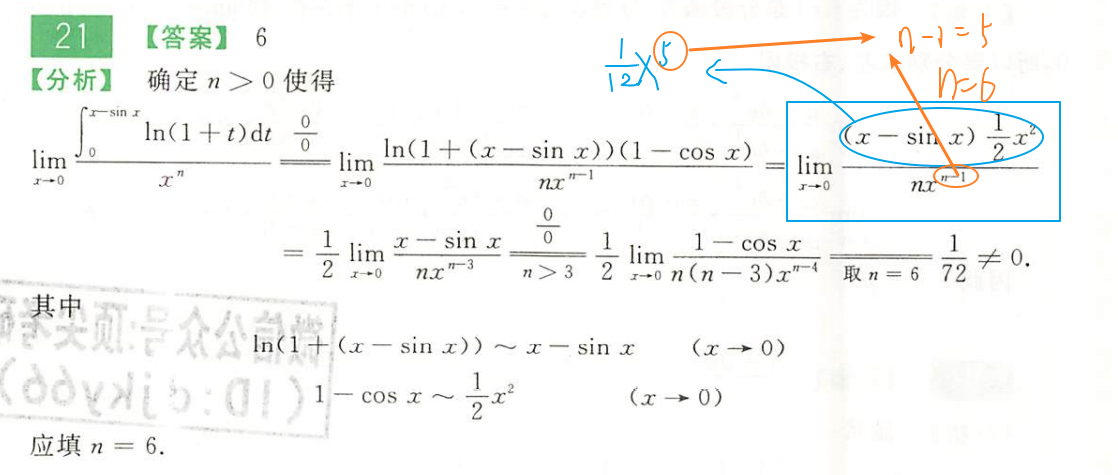
660-P8-T22
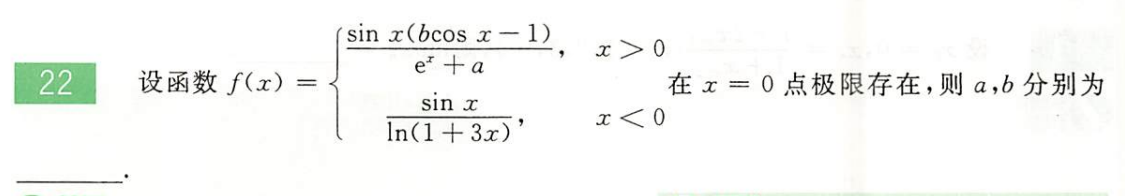
这道题的知识点在于分段函数在分界点处极限存在的问题。那么同样考虑极限存在定义中左右极限的问题,左极限与右极限分别列式子求出a,b即可。

660-P8-T23

这道题涉及到的知识点第一个就是单个函数连续性的问题以及连续性运算法则。

660-P8-T24

这道题涉及到的知识点有间断点的来源问题
- 分段函数的分界点(可能)
- 函数f(x)无定义的点(一定)
那么显然可以看出,a和b一定是e和1,所以现在的方法就可以进行代入验证。

660-P8-T25
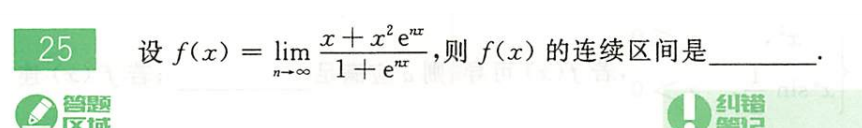
还是出现了
为什么会出现几个部分因为有

660-P8-T26
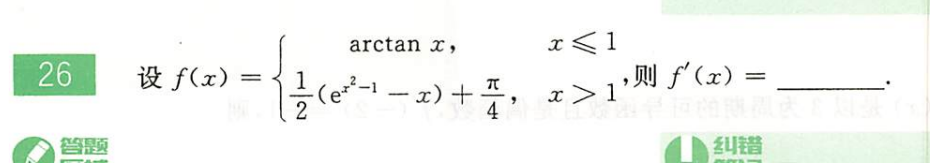
同样分段函数就分情况就讨论即可,而关于x=1这一点,用定义解决即可。

660-P8-T27


660-P8-T28


660-P8-T29

这道题运用到了f(x)与f'(x)奇偶性与周期性的问题。

660-P8-T30