Table of Contents
回顾
单双链表操作
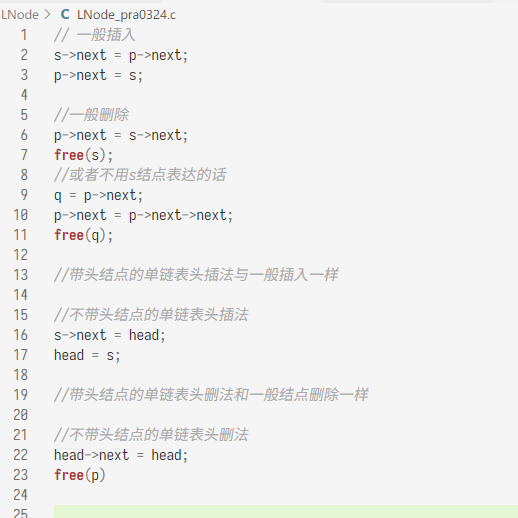
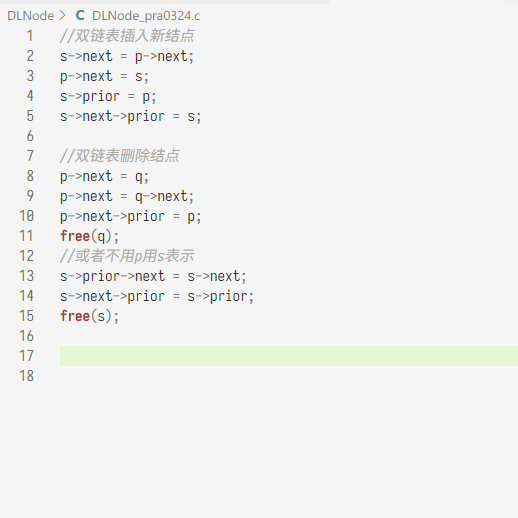
恋词复习U1,U2,U3
- regime n.政权;政体;管理制度
- entrenched adj.根深蒂固的
微分方程(一)
常微分方程的基本概念
- 微分方程
eg: y'=2x - 微分方程的阶
y''+y'^3 = x,阶为2 - 微分方程的解
有y=f(x)=x^2使y'=2x成立 - 微分方程的通解
有y=f(x)=x^2+c 使y'=2x成立 - 微分方程的特解
- 初始条件
- 积分曲线
一阶微分方程
- 可分离变量的方程
- 齐次微分方程
- 一阶线性微分方程
- 伯努利方程
- 全微分方程
可降阶的高阶方程
高阶线性微分方程
- 线性微分方程的解的结构
- 常系数齐次线性微分方程
- 常系数非齐次线性微分方程
- 欧拉方程
恋词U4
- press forward 加紧进行;决心继续;努力前进
- compress v.压紧;压缩
- profile n.侧面;侧面像;轮廓
- designate v.指明;指定
- commute v.上下班往返;通勤 n.上下班路程
- shareholding n.股东
- threshold n.门槛;入门;开端
- transformer n.变压器
- transplant v.(器官)移植;使迁移
- transaction n.(一笔)交易;业务
- transparent adj.透明的;明晰的;易识破的
- set aside 挑出;拨出;留出;不理会
- ideology n.意识形态
补充
今晚自习快结束的时候,鹅问了我一个问题,根本问题就是拐点的定义问题。 这里重新复习一下。
拐点的必要条件:设y=f(x)在点X0处二阶可导,且点(X0,f(X0))为曲线y=f(x)的拐点,则f''(X0)=0。
拐点第一充分条件:设y=f(x)在点X0的某去心邻域内二阶可导,且f''(x) = 0(或f(x)在X0处连续)
- 若f''(x)在x的左右两侧异号,则点(X0,f(X0))为曲线y=f(x)的拐点。
- 若f''(x)在x的左右两侧同号,则点(X0,f(X0))不是拐点。
拐点第二充分条件:设y=f(x)在点X0处三阶可导,且f''(X0)=0;
- 若f'''(X0)≠0,则点(X0,f(X0))为曲线y=f(x)的拐点。
- 若f'''(X0)=0,不能判定。
所以单单有二阶连续,且f''(X0)=0,不能推其为拐点(还要考虑两侧是否变号)。