没事啦
回家做了MR检查,嗯这里顺便科普一下,这里MR指的是MRA和MRI,嗯我照了两个。
磁共振成像(MRI)提供人体内部的一般成像,而磁共振血管造影(MRA)提供血管的特定图片。 MRA扫描使用MRI技术,但与常规MRI研究相比,其聚焦范围更窄。 MRI和MRA之间的主要区别在于它们的预期用途和应用,因为MRA用于非常特定的目的,而MRI可以在许多不同的环境中使用。
九百大洋,好家伙。最后也当然是什么事都没有,但是医生说我的脑结构和平常人不太一样,大概就是本来中线贴紧的,但是我是中间分开的,不过没有什么影响,并且我的血管也是非常好的。那么初步诊断应该就是偏头痛,这是现在很多人都会出现的问题了吧,嗯也的确困扰了我几年了,头痛起来真什么事都做不了。
希望身边的人身体健康,快快乐乐!!
定积分(一)
嗯,时隔多日,开始新一章的学习啦,继续加油!!
定积分的概念
定积分的定义。
,定积分是一个数,是特殊的合式极限(注意和不定积分做对比,不定积分是原函数的全体,是一个族)。
定积分存在的充分条件。
若f(x)在[a,b]上连续,则存在。若f(x)在[a,b]上有界且只有有限个间断点,则必定存在。若f(x)在[a,b]上仅有有限个第一类间断点。
定积分的几何意义
看图把!
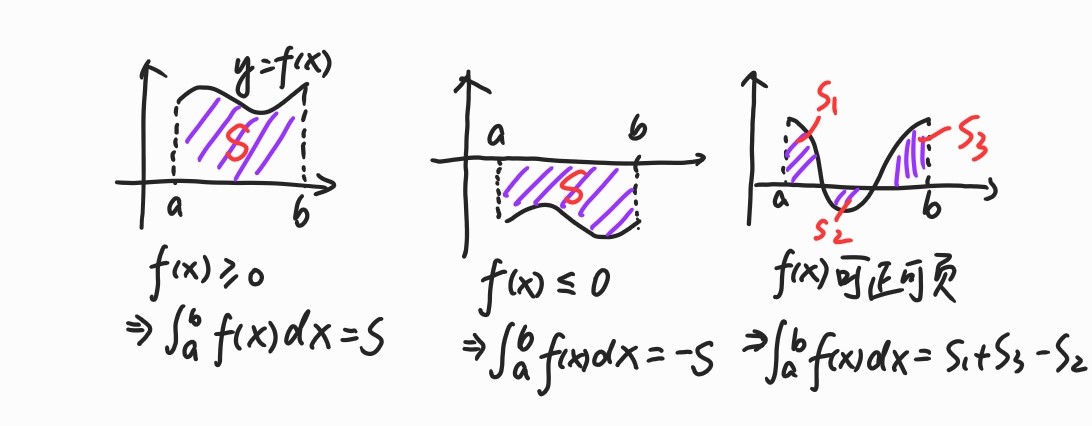
定积分的性质
不等式性质。
- 若在区间[a,b]上f(x)≤g(x),则
。
- 若M及m分别是f(x)在[a,b]上的最大值和最小值,则m(b-a)≤【】≤M(b-a),用图去理解吧。
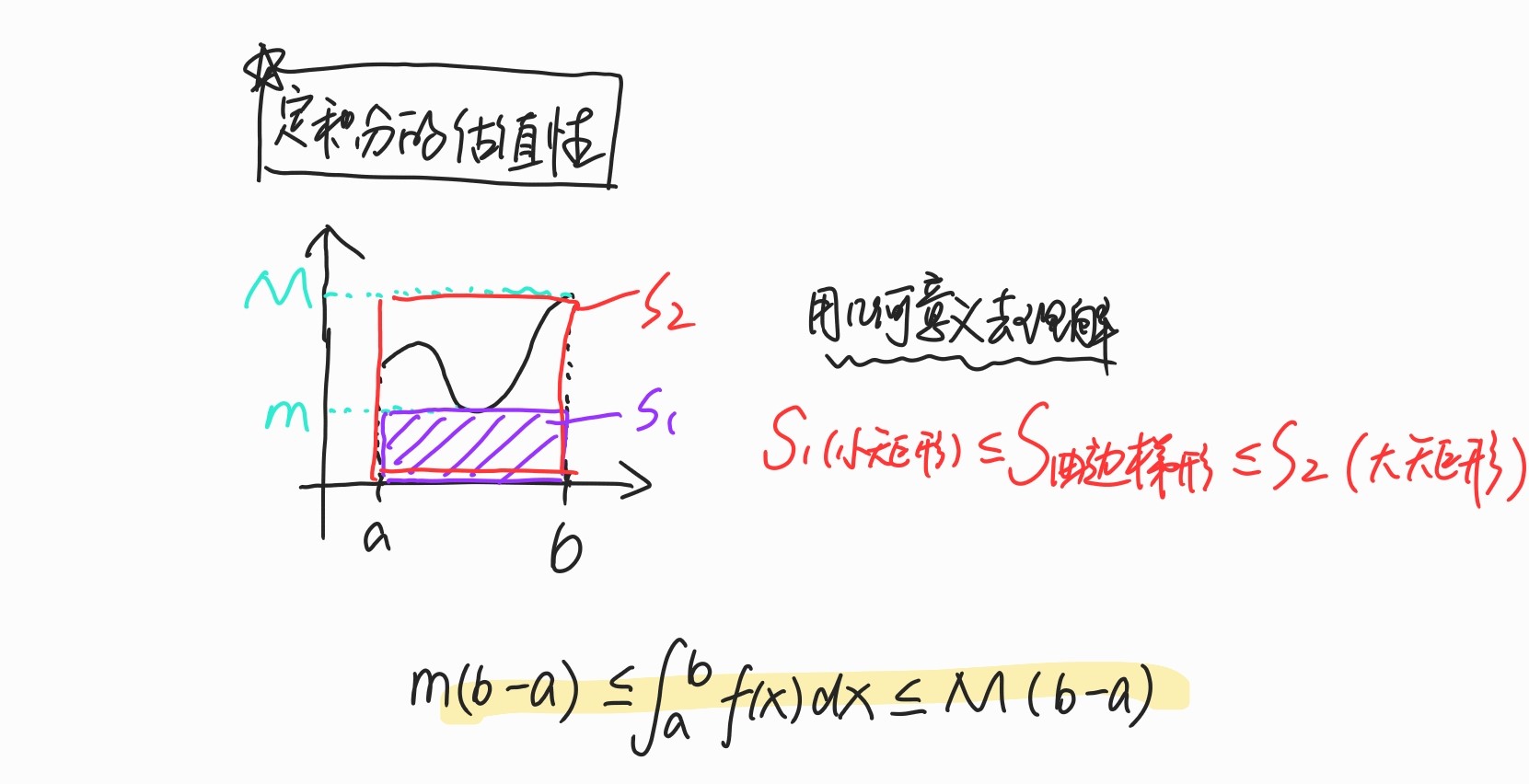
,积分的绝对值不超过绝对值得积分。类似于
|a+b|≤|a|+|b|。
中值定理
- ①若f(x)在[a,b]上连续,则
。这里的
f(ξ)几何意义上来理解相当于平均高度(平均值)。 - ②若f(x),g(x)在[a,b]上连续,g(x)不变号,则
。
⚠这里要说明的是,①是②的特例,当②中g(x)=1时即为①。
积分上限的函数
定义
变上限的积分 时是其上限x的函数(也就是表示一个新的函数),常称之为积分上限函数。
定理
- 微积分第一基本定理:设f(x)在[a,b]上连续,则
在[a,b]上可导且
。这个定理反映出两个重要性:①微分与积分的关系,互为逆运算。②原函数的存在性。
- 定理2:设函数f(x)在[-l,l]上连续,则①如果f(x)为奇函数,那么
必为偶函数。②如果f(x)为偶函数,那么
必为奇函数。
定积分的计算
- 牛顿-莱布尼兹公式:
,意义在于把定积分的计算归结于找被积函数的原函数。
- 换元积分法:
,换元时记得积分上下限也要换!
- 分部积分法:与不定积分类似,怎么用,何时用。
- 利用奇偶性和周期性:(奇函数面积抵消,偶函数面积“单边乘2”)。
- 利用公式
重要!!。