20210130

导数的概念

1. 导数实际上就是变化率（所以高数课本引入的例子一般为变速直线运动的瞬时速度，曲线在这一点的切线的斜率等）
2. 导数的定义有几种形式：

• 增量形式
• 
• 做题的时候根据题目条件选用最合适的导数定义形式即可！

3. 左右导数的定义。导数跟这一点有关，又因为Δx有正有负，所以这一点导数既跟这一点函数值有关，也跟这一点左右邻域函数值有关
4. 定理：函数f(x)在点x0处可导的充分必要条件使它在该点处左导数和右导数都存在且相等。

5. 若f(x)在区间(a,b)内可导，且 和 都存在，则称f(x)在区间[a,b]上可导。
6. 复习全书基础篇P32例1，就是典型的运用上面的定理即分段函数在分界点是否可导的问题，那么具体到题目中就是求x=1处左右导数，值得注意的是，在运用左右导数定义求左右导数结果的是，求右极限的时候f(1)的值仍是代入 求，而并非代入 x2 中求，因为1这一点只定义在 上。
7. 复习全书基础篇P32例2，这类题型一般要用定义做。首先根据题目条件选择最合适导数定义形式，很明显题目所给条件f(1+x) = af(x)，则选择增量形式的导数定义形式，然后利用 和 的定义，再根据题目条件进行结果的转换即可。（这道题典型的考导数定义的题目）

微分的概念

1. dy = AΔx。微分是什么？实际上dy就是函数改变量的近似值（即函数的增量的近似值），即dy≈Δy。再具体讲就是微分是函数改变量的“线性主部”（1.线性函数 2. 主要部分），可以参考高数书P84的正方形金属薄片膨胀的例子。
2. 定理：函数y=f(x)在点x0处可微的充分必要条件是：f(x)在点x0处可导，且有： 。

3. 复习全书基础篇P33例3，得到一个更加一般的结论：如果 ≠ 0，则dy和Δx为同阶无穷小。（如果这一点导数不为0，微分与自变量改变量为同阶无穷小。）

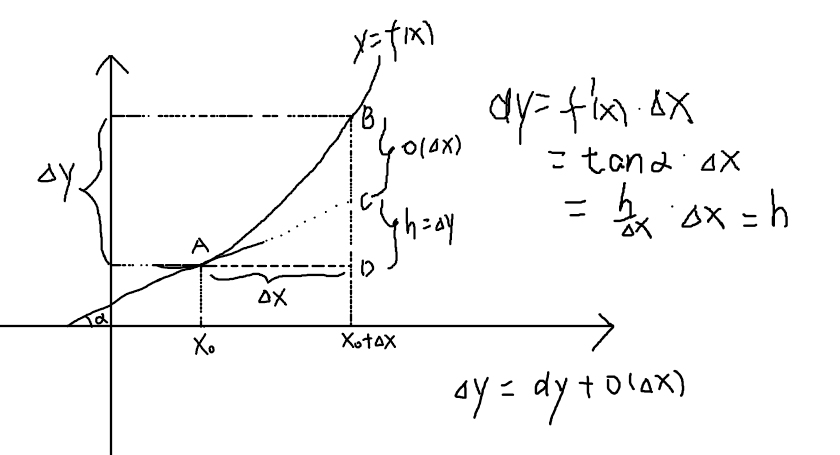
导数与微分的几何意义

1. 导数 在几何上表示曲线y=f(x)在点(x0,f(x0))处的切线的斜率。
2. 微分 在几何上表示曲线y=f(x)的切线上的增量。

3. 复习全书基础篇P33例4，搞清楚逻辑关系。先由垂直的这条直线求得切线方程的斜率，再由斜率得到这一点的x,y坐标，最后列出切线方程即可。

连续、可导、可微之间的关系

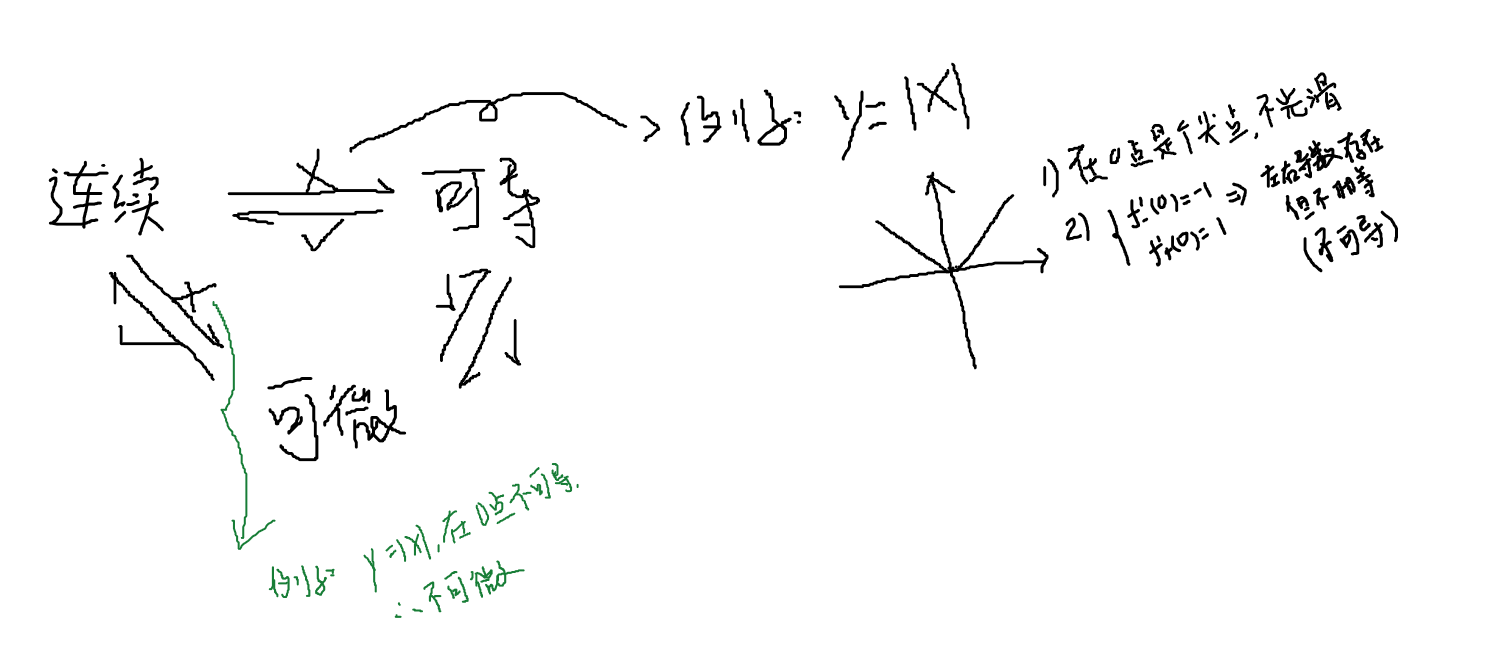
1. 值得注意的是，可导可微与连续的关系是一样的，因为可导肯定能推出可微，可微肯定能推出可导。

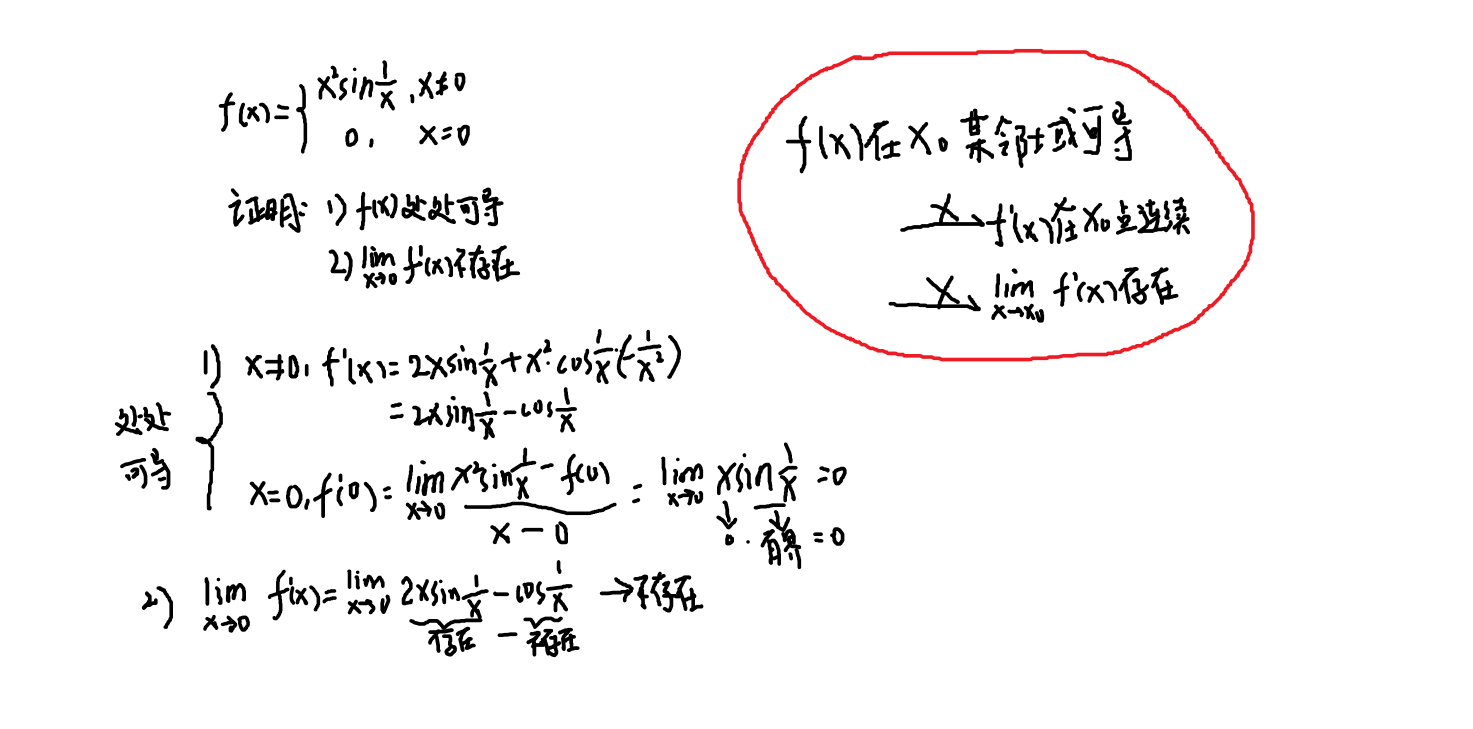
2. 上面这个反例用来证明n阶可导推不出n阶导函数存在，对应题目可以有第一章中的例33中的使用洛必达法则的时候注意事项。
   • f(x)n阶可导：
   • f(x)有n阶连续导数：

这道题二阶可导，只能用到2-1阶，即只能洛必达一次，不能再用第二次了，接下来如果还是0/0型极限，再用导数的定义即可。

3. 复习全书基础篇P34例5，分析题目的考点？在某点可导的定义是什么？具体到题目，要运用题目的条件，不难先发现C、D选项，因为可导，可导一定连续，连续极限一定存在且为这一点的函数值，那么题目所给条件即可等价于f(0)=0接着进行等式的变形即可。这道选择题还可以采用排除法，选择具体的函数进行排除，比如说A选项可举f(x)=|x|，D选项举f(x)=x即可。

书到了

李诞的书到了，《候场》献给大家，也献给我自己。